Wave Interactions at Surface of Discontinuity
Hongbin Ju
Department of Mathematics
Florida State University, Tallahassee, FL.32306
www.aeroacoustics.info
Please send comments to: hju@math.fsu.edu
In an uniform mean flow, linear waves of
vorticity, sound, and heat propagate independently. They only couple at
boundaries. If the mean flow is not uniform, waves will be diffracted by the
mean flow gradient, different waves may interact with each other, and new wave
modes may be generated.
To simply the problem, in this chapter we
will discuss a special case of the nonuniform mean flow: surface of
discontinuity (interface). Media on each side of the surface are uniform, in
which analytical wave solutions apply. Across the surface one or more flow
parameters are discontinuous. At the surface partial differential equations
break down. Integral equations have to be used to establish the relations
between the solutions on both sides. The final solutions are obtained by
matching solutions at the surface according to these relations.
The interface itself is assumed to be
stable in this chapter.
Surface of Discontinuity
Assume
the surface of discontinuity is steady on the ![]() plane at
plane at ![]() . (If the interface moves at a constant velocity, the
coordinate system can be established moving with the same speed so that the
interface is steady in this coordinate.) Across the interface derivatives and
partial differential equations donıt apply. However, mass, momentum, and energy
of the flow must be conserved. Therefore one should use the integral form of
the Euler equations. Suppose there is no mass injection, no external force or
heat, and no viscous effects, then integral conservative equations for mass,
momentum, and energy are (cht23.doc):
. (If the interface moves at a constant velocity, the
coordinate system can be established moving with the same speed so that the
interface is steady in this coordinate.) Across the interface derivatives and
partial differential equations donıt apply. However, mass, momentum, and energy
of the flow must be conserved. Therefore one should use the integral form of
the Euler equations. Suppose there is no mass injection, no external force or
heat, and no viscous effects, then integral conservative equations for mass,
momentum, and energy are (cht23.doc):
![]() ,
(1)
,
(1)
![]() ,
(2)
,
(2)
![]() .
(3)
.
(3)
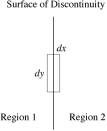
Fig.1, Steady surface of discontinuity.
Choose a fluid element with volume ![]() as in Fig.1.
From continuity equation (1) we have:
as in Fig.1.
From continuity equation (1) we have:
 . (4)
. (4)
Square bracket represents the difference
of a quantity at the two sides of the interface, ![]() . Similar equations can be established for momentum and
energy equations (2) and (3).
. Similar equations can be established for momentum and
energy equations (2) and (3).
As ![]() we have
we have
![]() ,
(5)
,
(5)
![]() ,
, ![]()
![]() , (6)
, (6)
![]() .
(7)
.
(7)
Quantities in square brackets must be
continuous across the interface. These are the matching conditions (boundary
conditions BCs) for the solutions at the two sides of the interface.
Tangential discontinuity
There are two types of discontinuities
depending on whether there is flow across the interface.
If there is no flow across the
discontinuity surface, BCs (5)~(7) becomes:
![]() , (8)
, (8)
![]() ,
(9)
,
(9)
![]() .
(10)
.
(10)
Across the interface pressure and heat must be continuous. Tangential velocities and density can be discontinuous:
![]() ,
, ![]() ,
, ![]() . (11)
. (11)
This is called tangential
discontinuity.
Normal Discontinuity and Shock Wave
The second type of discontinuity is when mass
flux across the interface is not zero. Then:
![]() ,
(12)
,
(12)
![]() ,
(13)
,
(13)
![]() ,
(14)
,
(14)
![]() ,
, ![]() ,
(15)
,
(15)
![]() . (16)
. (16)
For a perfect gas,
![]() ,
, ![]() .
.
If the perfect gas is adiabatic (![]() ), with Eq.(13), energy BC (16) is simplified to:
), with Eq.(13), energy BC (16) is simplified to:
![]() .
(17)
.
(17)
Equations in (15) show that tangential
velocities must be continuous at the interface. Pressure, density, and normal
velocity can be discontinuous. This is called normal discontinuity.
If any three of the six variables: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , are known, the other three can be explicitly expressed by
solving Eqs.(13), (14), and (17). One example of normal discontinuity is when
, are known, the other three can be explicitly expressed by
solving Eqs.(13), (14), and (17). One example of normal discontinuity is when ![]() is supersonic.
It is called shock wave, or shock, also called compression discontinuity. Since
tangential velocities are continuous, one can always establish the coordinate
in which the shock wave front is stationary and the flows on both sides are
perpendicular to the shock surface. This shock is called normal shock.
is supersonic.
It is called shock wave, or shock, also called compression discontinuity. Since
tangential velocities are continuous, one can always establish the coordinate
in which the shock wave front is stationary and the flows on both sides are
perpendicular to the shock surface. This shock is called normal shock.
For the normal shock, solving equations (13),
(14), and (17), one can obtain the Rankine-Hugoniot relations in terms of ![]() (Landau&Lifshitz1959, p.331):
(Landau&Lifshitz1959, p.331):
![]() , (18)
, (18)
![]() ,
(19)
,
(19)
![]() , (20)
, (20)
![]() .
(21)
.
(21)
Any one of the two sets of equations, (13)~(16)&(17),
or (18)~(21), can be used in applications. Sometimes it is more convenient to combine
the two sets of equations in analysis.
If in the coordinate system tangential
velocities are not zero, the above equations still hold except that the
velocity in the equations is the normal velocity to the shock. Total velocities
on both sides arenıt perpendicular to the shock wave; therefore it is called
oblique shock. An oblique shock can always be transformed into a normal shock by
establishing a coordinate system moving with the tangential velocity along the
surface.
Unsteady Surface
of Discontinuity
Now we will discuss unsteady surface of
discontinuity. Suppose the
surface of discontinuity without disturbance is at ![]() as in Fig.2. (It
shouldnıt matter whether the surface is horizontal or vertical. We use a
horizontal surface here just to show how to develop the formulas in a
coordinate system different from Fig.1.) After disturbed, the unsteady interface
is at position
as in Fig.2. (It
shouldnıt matter whether the surface is horizontal or vertical. We use a
horizontal surface here just to show how to develop the formulas in a
coordinate system different from Fig.1.) After disturbed, the unsteady interface
is at position![]() . A local coordinate system
. A local coordinate system ![]() is established
at the interface with
is established
at the interface with ![]() tangential to
the interface and
tangential to
the interface and ![]() normal to the
interface.
normal to the
interface.
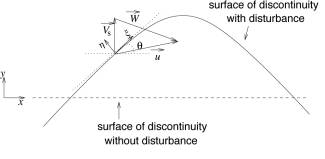
Fig.2, Unsteady surface of discontinuity.
A scalar is invariant in different
coordinate systems. A vector, however, changes its component coordinates in
different systems. In the ![]() coordinate
system, flow velocity is
coordinate
system, flow velocity is ![]() , and velocity of the interface is
, and velocity of the interface is
![]() ,
, ![]() ,
, ![]() : unit vector in y.
(22)
: unit vector in y.
(22)
In the ![]() system,
system,
![]() ,
, ![]() ,
(23)
,
(23)
![]() ,
, ![]() ,
,
where ![]() .
.
Flow velocity in the ![]() system is
system is
![]() ,
,
![]() , (24)
, (24)
![]() , (25)
, (25)
Derivative in the normal direction of the
interface is:
![]() .
(26)
.
(26)
If the disturbance is small, equations (23)~(26)
can be approximated at![]() :
:
![]() ,
,
![]() ,
, ![]() ,
(27)
,
(27)
![]() ,
, ![]() ,
(28)
,
(28)
![]() ,
(29)
,
(29)
![]() ,
(30)
,
(30)
![]() . (31)
. (31)
These are the relations between the two
coordinate systems we will need.
The ![]() system is not an
inertial system. The conservation laws in this moving volume must be established
in the
system is not an
inertial system. The conservation laws in this moving volume must be established
in the ![]() system
(cht23.doc):
system
(cht23.doc):
![]() ,
(32)
,
(32)
![]() ,
(33)
,
(33)
![]() . (34)
. (34)
A similar fluid element as in Fig.1 can
be established at the unsteady interface in Fig.2. Therefore across the interface
at ![]() :
:
![]() ,
(35)
,
(35)
![]() , i.e.,
, i.e., ![]() ,
, ![]() , (36)
, (36)
![]() .
(37)
.
(37)
For tangential discontinuity
at ![]() ,
,
![]() , or
, or ![]() ,
(38)
,
(38)
![]() ,
(39)
,
(39)
![]() .
(40)
.
(40)
Expand p at ![]() ,
,
![]() .
.
If the disturbance is small then
![]() at
at ![]() .
.
Further using (27) ~ (31), equations (38)~(40)
can be rewritten in terms of variables in the ![]() system at
system at ![]() :
:
![]() ,
(41)
,
(41)
![]() , (42)
, (42)
![]() . (43)
. (43)
It is noted that all the variables are
total variables which are the sum of mean variables and perturbations. These
three equations are the kinematic and dynamic boundary conditions at the
mean surface of tangential
discontinuity. Across the mean interface at![]() , pressure must be continuous [Eq.(42)]. Although velocity
normal to the unsteady interface (
, pressure must be continuous [Eq.(42)]. Although velocity
normal to the unsteady interface (![]() ) is continuous [Eq.(38)],
) is continuous [Eq.(38)], ![]() is not
necessarily continuous. Instead Eq.(41) implies the continuity of displacement:
is not
necessarily continuous. Instead Eq.(41) implies the continuity of displacement:
![]() . (44)
. (44)
To prove it, we define function ![]() :
:
![]() .
.
![]() at the
interface,
at the
interface, ![]() in medium 1, and
in medium 1, and
![]() in medium 2. At
the interface
in medium 2. At
the interface ![]() ,
,
![]() , or,
, or,
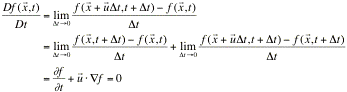
Since ![]() ,
, ![]() ,
, ![]() , Eq.(41) is recovered.
, Eq.(41) is recovered.
Eqs.(41)~(43) are the
boundary conditions for immiscible flows such as air and water. Sometimes this
model is extended to other situations. For a jet, the two sides of the
interface separating the jet and its environment may have the same gas. However
the gas is often assumed immiscible at the interface, so that tangential
discontinuity across the interface is applicable. Another example is plug flow
over an impedance wall. The impedance wall is often considered a surface of
tangential discontinuity with continuous displacement.
For normal discontinuity, Eqs.(35)~(37) are,
![]() ,
(45)
,
(45)
![]() ,
(46)
,
(46)
![]() ,
(47)
,
(47)
![]() ,
(48)
,
(48)
![]() .
(49)
.
(49)
For small disturbance, at ![]() :
:
![]() , (50)
, (50)
![]() , (51)
, (51)
![]() , (52)
, (52)
![]() . (53)
. (53)
These four equations are the matching conditions
for normal discontinuity with small disturbance.
Acoustic Wave Transmission (Refraction)
at Surface of Density Discontinuity
As
the first example, we discuss the sound wave reflection/refraction at an
interface of two immiscible media such as air and water as in Fig.3. The two
fluids are assumed ideal, adiabatic, and quiescent (![]() ,
, ![]() ). The interface is steady before sound is introduced from
medium 1. Since there is no flow across the interface, the interface has
tangential discontinuity. When there is no sound, pressure is continuous across
the interface [BC (9)]:
). The interface is steady before sound is introduced from
medium 1. Since there is no flow across the interface, the interface has
tangential discontinuity. When there is no sound, pressure is continuous across
the interface [BC (9)]:
![]() .
(54)
.
(54)
Density is discontinuous, and so is sound speed:
![]() ,
, ![]() .
(55)
.
(55)
Impedance
of a uniform medium to sound is ![]() . Eq.(55) means there is impedance mismatch at the interface,
which inevitably gives rise to sound reflection/refraction.
. Eq.(55) means there is impedance mismatch at the interface,
which inevitably gives rise to sound reflection/refraction.
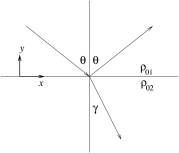
Fig.3, Sound
transmission at surface of density discontinuity.
The interface itself is assumed stable. If there is gravity, the lighter fluid must be on the top of the heavier fluid, otherwise the interface will have Rayleigh-Taylor Instability.
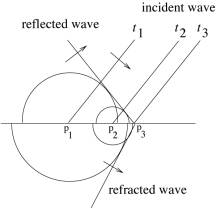
Sound
wave, introduced into the first medium, propagates towards the interface at an
angle ![]() as in Fig.3. At
the interface part of the sound wave is reflected back and part of it transmits
into the second medium. The interface is perturbed with displacement
as in Fig.3. At
the interface part of the sound wave is reflected back and part of it transmits
into the second medium. The interface is perturbed with displacement ![]() .
.
When disturbance is small, tangential discontinuity
requires continuous pressure and displacement across the interface at ![]() [Eqs.(42)&(44)].
Normal velocity is generally not continuous. However, when there is no mean flow, normal velocity is continuous
according to Eq.(41). Therefore the dynamic and
kinematic boundary conditions of disturbance (the prime is omitted) at
[Eqs.(42)&(44)].
Normal velocity is generally not continuous. However, when there is no mean flow, normal velocity is continuous
according to Eq.(41). Therefore the dynamic and
kinematic boundary conditions of disturbance (the prime is omitted) at ![]() are:
are:
![]() ,
(56)
,
(56)
![]() .
(57)
.
(57)
There
is no vortical motion in the ideal, quiescent medium according to cht1.doc and
cht7.doc. General acoustic solution in an ideal, quiescent medium with density ![]() and sound
velocity
and sound
velocity ![]() has been given by
Eqs.(22)~(24) in cht1.doc. The solutions are:
has been given by
Eqs.(22)~(24) in cht1.doc. The solutions are:
![]() ,
(58)
,
(58)
![]() ,
(59)
,
(59)
![]() ,
(60)
,
(60)
![]() .
(61)
.
(61)
The equation of computing ![]() from
from ![]() is in cht1.doc.
If
is in cht1.doc.
If ![]() is real and
is real and ![]() , the wave is a pure propagating plane sound wave. If
, the wave is a pure propagating plane sound wave. If ![]() is real but
is real but ![]() or
or ![]() , the wave only propagates in x direction with phase speed
, the wave only propagates in x direction with phase speed ![]() , with decaying amplitude in y direction. For all other
, with decaying amplitude in y direction. For all other ![]() , the wave is decayed plane wave propagating in an oblique
direction. Except for the propagating waves, effect of disturbances is only
local to the interface.
, the wave is decayed plane wave propagating in an oblique
direction. Except for the propagating waves, effect of disturbances is only
local to the interface.
Incident wave
Assume
the incident wave is a propagating wave with incident wave angle ![]() to the normal
direction (Fig.3):
to the normal
direction (Fig.3):
![]() ,
, ![]() ,
, ![]() ,
(62)
,
(62)
![]() ,
, ![]() ,
, ![]() .
(63)
.
(63)
To
ensure propagating wave in +x direction,
![]() must be real and
must be real and
![]() , then
, then ![]() is also real,
and the reflected wave is a propagating wave.
is also real,
and the reflected wave is a propagating wave.
Reflected wave
From Eqs.(56)&(57), the reflected
wave and transmitted wave must have the same ![]() as the incident
wave. Thus the reflected wave solutions are:
as the incident
wave. Thus the reflected wave solutions are:
![]() ,
, ![]() ,
, ![]() .
(64)
.
(64)
Refracted wave
The transmitted (refracted) wave
solutions are:
![]() ,
, ![]() ,
, ![]() .
(65)
.
(65)
Suppose the incident wave is from the
medium with smaller density, i.e.,
![]() . Since
. Since ![]() , we have
, we have ![]() . For the propagating incident wave,
. For the propagating incident wave, ![]() is real and
is real and ![]() . Therefore
. Therefore ![]() ,
, ![]() is real and thus
the refracted wave is a propagating wave in the direction with angle
is real and thus
the refracted wave is a propagating wave in the direction with angle ![]() as in Fig.3. In
this case the refraction wave solutions are:
as in Fig.3. In
this case the refraction wave solutions are:
![]() ,
, ![]() ,
, ![]() .
.
![]() ,
, ![]() ,
, ![]() .
(66)
.
(66)
The refracted wave angle is determined
by:
![]() .
(67)
.
(67)
This is the Snellıs law. When the incident wave is in the
lighter fluid, the refracted wave is bent towards the normal direction.
On the other hand, if the incident wave
is in the heavier fluid, then ![]() . Eq.(67) shows
the refracted wave is bent away from the normal direction. It is
possible that
. Eq.(67) shows
the refracted wave is bent away from the normal direction. It is
possible that ![]() , i.e.
, i.e. ![]() , for which no angle
, for which no angle ![]() can be
determined from (67) and
can be
determined from (67) and ![]() is a pure
imaginary complex number. In this case, the refracted wave only propagates in x direction (along the interface) with
phase speed
is a pure
imaginary complex number. In this case, the refracted wave only propagates in x direction (along the interface) with
phase speed ![]() , but the amplitude decays in -y direction. (Check out Fig. 12 in paper Tam&Ju, Computation of the
Aliasing and the Interface Transmission Benchmark Problems by the
Dispersion-Relation-Preserving Scheme, 4th CAA workshop
NASA/CP-2004-212954). There is a critical angle,
, but the amplitude decays in -y direction. (Check out Fig. 12 in paper Tam&Ju, Computation of the
Aliasing and the Interface Transmission Benchmark Problems by the
Dispersion-Relation-Preserving Scheme, 4th CAA workshop
NASA/CP-2004-212954). There is a critical angle,
![]() .
(68)
.
(68)
When the incident wave angle is bigger
than this angle, the incident wave will be totally reflected.
Reflection coefficient
Coefficients R and T in equations (64) and (65) can be determined from boundary conditions (56)&(57):
![]() ,
,
![]() .
.
Therefore,
![]() ,
(69)
,
(69)
![]() .
(70)
.
(70)
When ![]() and the incident
angle is larger than critical angle
and the incident
angle is larger than critical angle ![]() ,
, ![]() is purely
imaginary, and
is purely
imaginary, and ![]() , that means the incident wave is totally reflected.
, that means the incident wave is totally reflected.
Baroclinic vorticity production
The
two uniform media are vorticity free. However, as we know in cht5.doc, in a
region with nonuniform density, the mass center and the geometric center of the
a fluid element doesnıt coincide. When sound waves propagate into this region,
vorticity will be generated. This is called Baroclinic Vorticity Production. According to cht5.doc, the indicator
of vorticity generation is circulation instead of vorticity, since vorticity of
a material fluid element may change while the circulation does not. To
quantify the circulation at the surface of discontinuity, one may define the
circulation density ![]() as in Fig.4:
as in Fig.4:
![]()
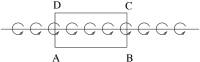
Fig.4, Circulation at the interface.
Than:
![]() .
(71)
.
(71)
Vorticity is generated because of the misaligned acoustic pressure and the mean density gradients.
Physical
explanation
Suppose
the wave front of the incident sound hits the interface at point p1
at time ![]() . It generates one cylindrical wave in medium 1 and one
cylindrical wave in medium 2. At
. It generates one cylindrical wave in medium 1 and one
cylindrical wave in medium 2. At ![]() the incident
wave front hits p2 and generates two other cylindrical waves, one on
each side of the interface. Fig.5 shows the wave pattern at time
the incident
wave front hits p2 and generates two other cylindrical waves, one on
each side of the interface. Fig.5 shows the wave pattern at time ![]() when the
incident wave just hits p3. At this time waves generated at previous
times (
when the
incident wave just hits p3. At this time waves generated at previous
times (![]() and
and ![]() ) have propagated. The envelope of these waves in medium 1
forms the reflected wave front; the envelope of the waves in medium 2 forms the
transmitted wave front. Sound speeds on both sides are different, so are angles
of the reflected and transmitted waves.
) have propagated. The envelope of these waves in medium 1
forms the reflected wave front; the envelope of the waves in medium 2 forms the
transmitted wave front. Sound speeds on both sides are different, so are angles
of the reflected and transmitted waves.
Fig.5, Sound wave
transmission at surface of density discontinuity at time ![]() .
.
Wave Interaction with Shock Wave
One-dimensional analysis of wave interaction with shock wave was given by Powell. In one dimension there is no vorticity wave and there is no sound wave propagating upstream in the supersonic medium. If the incident wave before the shock is a sound wave, two waves exist after the shock: the transmitted, amplified sound wave and the convective entropy wave. If the incident wave is an entropy wave, the downstream waves are transmitted entropy wave and intense sound wave.
In two or three dimensions, when a vortex hits the shock wave, there exist all three modes after the shock: vorticity wave, sound wave, and entropy wave. This is believed to be the mechanism of broadband shock associated noise in a supersonic jet. Vortex/shock interaction depends on whether the flow after the shock is subsonic or supersonic.
Vortex/shock
interaction can be investigated analytically by fitting the shock with
Rankine-Hugoniot relation. Moore1954 analyzed the interaction of a normal shock
with an oblique plane sound wave or vortex wave. Ribner discussed plane vortex
wave/shock interaction (Ribner1954) and cylindrical vortex with axis aligned
with the shock (Ribner1985). Erlebacher, Hussaini&Shu discussed cylindrical
vortex with axis normal to the shock (i.e.,
longitudinal vortex). Numerical investigation was done by many researchers,
such as Meadows, Kumar&Hussaini1991, Erlebacher, Hussaini&Shu, etc.
Suppose
the undisturbed shock is at ![]() . The flow comes in from region 1 to region 2. The BCs at
. The flow comes in from region 1 to region 2. The BCs at ![]() are from
(13)~(15)&(17):
are from
(13)~(15)&(17):
![]() , (72)
, (72)
![]() ,
(73)
,
(73)
![]() ,
(74)
,
(74)
![]() .
(75)
.
(75)
Or one can use Rankine-Hugoniot equations
(18)~(21) directly.
With small disturbance, the shock wave
surface is disturbed to position ![]() . The BCs satisfied at
. The BCs satisfied at ![]() Eqs.(50)~(53)
are linearized to be:
Eqs.(50)~(53)
are linearized to be:
![]() ,
(71)
,
(71)
![]() ,
(72)
,
(72)
![]() ,
(73)
,
(73)
![]() .
(74)
.
(74)
Upstream sound wave/shock interaction
Suppose
the incident wave from region 1 is a plane sound wave. According to Eqs.(61)~(64)
in cht1.doc, a plane sound wave can be represented by:
![]() ,
(75)
,
(75)
![]() ,
(76)
,
(76)
![]() ,
(77)
,
(77)
![]() ,
, ![]() .
(78)
.
(78)
Physical
variables in time domain are real parts of these variables in Eqs.(75)~(78). A and ![]() are amplitude (strength)
and annular frequency of the sound wave.
are amplitude (strength)
and annular frequency of the sound wave. ![]() is the wave
number in y direction. Wave
number in x direction is computed
by Eq.(66) of cht1.doc:
is the wave
number in y direction. Wave
number in x direction is computed
by Eq.(66) of cht1.doc:
![]() .
(79)
.
(79)
Check Fig.10 of cht1.doc for the branch cut.
No sound wave is reflected at the shock since the flow in region 1 is supersonic. The sound wave is refracted in region 2 behind the shock. Vorticity and entropy waves are generated at the shock. All the waves after the shock have the same frequency and wave number in y direction as the incident sound wave.
For the sound wave in region 2:
![]() ,
(80)
,
(80)
![]() , (81)
, (81)
![]() , (82)
, (82)
![]() ,
, ![]() .
(83)
.
(83)
Assume flow after the shock is subsonic, then,
![]() .
(84)
.
(84)
Solution of vorticity wave in region 2 is expressed by Eqs.(72)~(75) in Cht1.doc. They are:
![]() , (85)
, (85)
![]() ,
(86)
,
(86)
![]() ,
, ![]() ,
, ![]() .
(87)
.
(87)
where ![]() .
.
Entropy wave in region 2 is
represented by Eqs.(76)~(79) in cht1.doc:
![]() ,
, ![]() ,
, ![]() ,
(88)
,
(88)
![]() ,
, ![]() .
(89)
.
(89)
The total waves in region 2 are sum of these three waves:
![]() ,
(90)
,
(90)
![]() ,
(91)
,
(91)
![]() , (92)
, (92)
![]() ,
(93)
,
(93)
![]() .
(94)
.
(94)
Shock
wave displacement ![]() . Substitute incident wave Eqs.(75)~(78) and waves
after the shock Eqs.(90)~(93) into the four matching conditions, Eqs.(71)~(74).
From the four equations, B, C, D, and
. Substitute incident wave Eqs.(75)~(78) and waves
after the shock Eqs.(90)~(93) into the four matching conditions, Eqs.(71)~(74).
From the four equations, B, C, D, and ![]() can be solved in
terms of A.
can be solved in
terms of A.
Upstream plane vorticity wave/shock interaction
Suppose a plane vorticity wave is propagating towards the shock:
![]() , (95)
, (95)
![]() ,
(96)
,
(96)
![]() ,
, ![]() ,
, ![]() .
(97)
.
(97)
where ![]() .
.
The
three waves on the downstream of the shock wave can be expressed by equations (80)~(94).
Substitute incident wave Eqs.(95)~(97) and waves after the shock Eqs.(90)~(93)
into the four matching conditions, Eqs.(71)~(74), from which B, C, D, and ![]() can be solved in
terms of A.
can be solved in
terms of A.
Upstream plane entropy wave/shock interaction
If the upstream incident wave is a plane
entropy wave, then,
![]() ,
, ![]() ,
, ![]() ,
(98)
,
(98)
![]() ,
, ![]() .
(99)
.
(99)
In
the same way as before, B, C, D, and ![]() can be solved by
matching waves on both side of the shock.
can be solved by
matching waves on both side of the shock.
Downstream plane sound wave/shock interaction
Now
letıs discuss the case where incident wave is from downstream of the shock.
Since no wave can propagate upstream against the supersonic flow in region 1,
one has:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
(100)
.
(100)
The only possible incident wave from the downstream is sound. It is represented by equations:
![]() ,
(101)
,
(101)
![]() ,
(102)
,
(102)
![]() ,
(103)
,
(103)
![]() ,
, ![]() ,
(104)
,
(104)
where,
![]() .
(105)
.
(105)
The reflected waves are represented by Eqs.(80)~(89). The total waves in region 2 are:
![]() ,
(106)
,
(106)
![]() ,
(107)
,
(107)
![]() , (108)
, (108)
![]() ,
(109)
,
(109)
![]() .
(110)
.
(110)
Substitute
Eqs.(100) and (106)~(110) into the four matching conditions, Eqs.(71)~(74). B,
C, D, and ![]() can then be
solved in terms of A.
can then be
solved in terms of A.