Wave Generation by Oscillating Wall

in Static Media

Hongbin Ju

Department of Mathematics

Florida State University, Tallahassee, FL.32306

www.aeroacoustics.info

Please send comments to: hju@math.fsu.edu

Sound, vorticity wave and entropy wave are the three normal modes of linear Euler equations in uniform ideal flows (cht1.doc: Waves in Uniform Flow on Half Plane). In this chapter we will further consider viscous effects on the wave mode separation. It will be shown that, when a medium is static (no mean flow) and barotropic (density depends only on pressure), and perturbation is small so that linearity applies, acoustic and vortical motions can be unambiguously separated. They are only coupled at boundaries. If the boundary conditions are also separable, the two waves can then be totally decoupled.

The continuity and Navier-Stokes equations with isentropic process are:

, (1)

(2a)

, (2b)

. (3)

Viscous effects only appear in momentum equations. Two forms of momentum equations, (2a) and (2b), are given. In the second form, the net shear viscous force acting on a fluid element is expressed as the sum of gradient of dilation and curl of rotation. Heat produced by viscous stress is neglected so that isentropic relation Eq.(3) instead of the full energy equation is needed. No entropy wave is assumed in this chapter. The medium is barotropic, since for the isentropic process density depends only on pressure.

The perturbation is small. The linearized isentropic equation (3) is:

. (4)

p and are perturbed pressure and density. is the sound speed in the undisturbed medium. From now on variables with subscript '0' are for the static medium without perturbation. Variables without subscript '0' are perturbation variables.

The medium has no mean flow, . Linearizing equations (1), (2a) and (2b), one obtains:

, (5)

(6a)

. (6b)

in continuity equation (5) is substituted by p because of Eq.(4). Eq.(5) shows that pressure changing rate is only related to dilation of the fluid, which is true for all barotropic fluids. This turns out to be critical for the wave mode separation.

Separation of Waves

Separation of acoustic and vortical waves can be made by using the normal mode method (cht1.doc: Waves in Uniform Flow on Half Plane). Here we attempt to separate the waves based on their physical origins. As we know, acoustic waves are generated by oscillations of the fluid element under the balance of inertia and elastic restoring forces. On the other hand, shear stresses act tangentially at the surface of a fluid element, if they are unbalanced, will generate vortical waves. In momentum equations (6a)&(6b), there are two forces exerted on the fluid element surface: pressure and viscous shear stresses. Pressure is the elastic force since it changes as the result of contraction/expansion of the fluid element [Eq.(5)]. In a barotropic fluid, pressure doesn't generate any rotation (Thomson Theorem). For a fluid element has the same center of mass and geometry, and pressure force acts through this center generating no rotation (Panton1996, p.329). Therefore pressure serves solely as the elastic force for acoustic waves. The net shear viscous stress is related to rotation and dilation (Eq.6b). Dilation related viscous stress acts as friction to acoustic waves; rotation related viscous stress is the restoring force for vortical waves.

It is crucial to separate the two type of waves based on the dilation and rotation fields of the flow. A fluid element undergoes three different type of motions when forces exert on its surface: dilation (isotropic expansion/contraction) with volume change rate , rigid-body rotation with vorticity , and pure strain without volume change and rotation. Accordingly, velocity at any point in the flow can be decomposed into two parts:

. (7)

is the velocity associated with the dilation field of the flow:

, . (8)

is the velocity associated with the vorticity distribution of the flow:

, . (9)

Any velocity associated with pure strain can be added to and/or since it has no dilation and rotation. Therefore is the irrotational (vorticity free) velocity, and is the solenoidal (dilation free) velocity.

At this point we assume pressure can be decomposed accordingly:

. (10)

is associated with dilation field , and associated with vorticity field .

Plugging Eq.(7) and (10) into Eqs.(5)&(6) and equating terms with subscript ≥a≤ and terms with subscript ≥v≤, one obtains two sets of equations.

Acoustic wave

The equations about the irrotational field are:

, (11)

, (12)

. (13)

The second form of the momentum equation Eq.(6b) is used here for convenience. In Eq.(13), the inertia is mostly balanced by pressure, the restoring force for acoustic waves. Just as we said before, represents the vorticity free field. Its pure strain and the associated viscous stress are not necessarily zero. The viscous term in (13) is the net viscous stress due to dilation, which acts as friction to the acoustic wave.

Vortical Wave

The equations about the solenoidal field are:

, (14)

, (15)

. (16)

Momentum equation Eq.(6a) is convenient to use for the vortical mode. Integrating Eq.(15) gives . By taking divergence of (16), one obtains Laplace equation . There are no nonsingular solutions for Laplaceπs equation except . Generally vortexes are compact in space with in the far field. Therefore the solution to Laplaceπs equation is . The vortical wave equations become:

, (17)

, or, (18)

, (19)

where .

For ideal gas, viscous terms are dropped, then , , which means no vortical motion in ideal static medium.

Acoustic and vortical waves propagate independently in the static medium. This is true due to the linearity and uniform of mean flow. Nonlinearity or non-uniform mean flow will inevitably couple the two wave modes.

Acoustic waves and vortical waves only couple at boundaries where the total velocity and total pressure satisfy boundary conditions. In some simple situations, boundary conditions are also separable so that the two types of motions are totally decoupled in the whole field. In the following sections we will have four examples. In the first example a pure vortical wave is generated by a plane wall oscillating on its own plane. In the second example a pure acoustic wave is excited when the plane wall oscillates in its normal direction. In the third example, the wall oscillates in an oblique direction; the velocities of the wall in its tangential and normal directions drive vortical wave and sound wave respectively. In the last example, the oscillating body has an arbitrary shape; when oscillating frequency is in certain range, the boundary conditions can be approximately decoupled.

Stokes Layer

The simplest but most typical example of vortical wave is the wave generated by a plane wall oscillating in a viscous medium. The medium is bounded by an infinitive rigid wall on (x,z) plane in the three dimensional Cartesian system (x,y,z) shown in Fig.1. The wall oscillates on its own plane. The viscous wave is generated by the wall and propagates into the fluid.

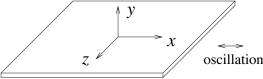
Fig.1, Wall oscillating on its own plane.

Analytical solution of the full incompressible N.S. equations for this problem was found by Stokes (G.G.Stokes1851). The viscous wave is called Stokes wave. Details of the solution is in the book of Landau&Lifshitz1959. Here we will solve this problem using the method of wave separation.

The wall starts to oscillate at in x direction. Asymptotically the wall vibrates harmonically at annular frequency , i.e., as :

, , , at ; (20)

, , , at .

We will assume harmonic solutions while still considering initial field static. Complex variables may be used in the analysis. As long as the equations are linear, the final result can be obtained by taking real parts of complex quantities.

Acoustic Wave

We first show that the oscillation of the wall on its own plane will not drive sound waves.

Boundary condition (20) has no dependence on x and z. From physics intuition of symmetry, all variables will only depend on y and t. Momentum equations in x and z directions from Eq.(13) are:

, . (21)

Initially there is no sound in the field. This immediately gives:

, . (22)

Eq.(12) and momentum equation (13) in y direction become,

, (23)

. (24)

By eliminating in Eqs.(23) and (24), the sound wave equation about is:

. (25)

It will be shown in the vortical wave analysis next Eq.(29), . Then boundary condition (20) means:

, at and . (26)

The solution of Eq.(25) with boundary (26) is

, . (27)

Viscous stress from the oscillating wall doesnπt squeeze fluid and thus generates no sound waves.

Vortical Wave

The vortical velocity is dilation free [Eq.(14)], therefore:

. (28)

From momentum equation (18) and Eq.(28):

. (29)

Initially there is no vortex, therefore vortical velocity in y direction is always zero no matter what boundary conditions are:

. (30)

Momentum equation (18) in z direction is:

. (31)

Its solution for at and is:

. (32)

Momentum equation in x direction:

. (33)

We have already shown in acoustic wave solution Eq.(22), . From (20), the boundary condition for becomes:

, at ; (34)

, at .

Eq.(33) with boundary conditions (34) can be solved by using the normal mode method. Assuming this form of solution:

. (35)

Substituting it into (33), we obtain the dispersion relation:

. (36)

Suppose is real, then,

, . (37)

k with negative sign should be removed since it gives a solution with exponential growth as . Then the solution is:

. (38)

This describes a transverse wave in the viscous fluid with the propagation direction perpendicular to the oscillation direction. is penetration depth of the wave propagating into the medium. A thin boundary layer, called Stokes layer, is formed near the wall. Within this boundary layer, sufficient resolution must be warranted if numerical methods are used to solve this problem.

Eqs.(17), (30), (32), and (38) form the full set of vortical solutions to the Stokes layer problem. The oscillation of the uniform viscous stress on the medium by the wall doesn't squeeze the fluid and thus generates no sound. When the viscous stress is non-uniform, sound can be generated. This is consistent with Lighthillπs Analogy Theory in which the sound source is the double divergence of viscous stresses: .

The equations we solved are linearized continuity equation (5) and N.S. equations (6). However, this set of solutions also satisfy the full incompressible N.S. equations (Landau&Lifshitz1959) and the full compressible N.S. equations with isentropic relationship, Eqs.(1)~(3). The reason is that for these solutions, nonlinear term in the N.S. equations is zero. Therefore the full N.S. equation is linear no matter if the oscillation is weak or strong.

Similar solutions can be found for an oscillating cylinder around its axis, or an oscillating sphere around its center.

Plane Wall Oscillation in Normal Direction

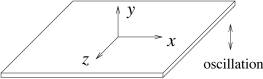
Fig.2, Plane wall oscillating in normal direction.

Now letπs discuss the wave generated by a plane wall oscillating in its normal direction as in Fig.2. The boundary conditions are:

, , , at ; (39)

, , , as .

The boundary conditions have no dependence on x and z. The solutions are only functions of y and t.

For the same reason as in the last section, acoustic velocities in x and z directions are:

, . (40)

Eq.(25) is the wave equation for . Eq.(30) still holds, then the boundary condition about based on (39) is:

, at ; (41)

, as .

Assume the next form of solution:

. (42)

Substituting it into Eq.(25), we obtain the dispersion relation:

. (43)

For real ,

. (44)

k with + sign represents decay waves as . The branch cut for the square root is shown by Fig.3.

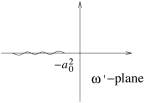
Fig.3, Branch cut for on plane.

Acoustic pressure is obtained from Eq.(12):

. (45)

Eqs.(40), (42) and (45) form the acoustic solution of the problem. It can be shown that the wall oscillating in its normal direction does not generate vortical waves.

Plane Wall Oscillation in Oblique Direction

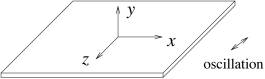
Fig.4, Plane wall oscillating in oblique direction.

Suppose the wall oscillates in an oblique direction as in Fig4. At the boundary,

, , , at . (46)

, , , as .

We have already known that oscillation of the plane wall in its normal direction does not drive vortical waves, and oscillation of the wall on its own plane does not drive sound waves. Therefore, at the wall drives only sound wave with solutions (40), (42) and (45). at the wall drives only vortical wave with solutions (17), (30), (32), and (38).

Oscillation of Object with Arbitrary Shape

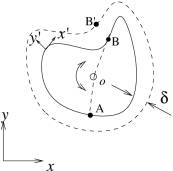
Fig.5, Oscillation of an arbitrary object.

As the oscillating object has an arbitrary shape as in Fig.5, the analyses for plane walls in previous sections do not apply since flow variables are no longer only functions of y and t. However, if the object surface is smooth and the oscillation frequency is high, the acoustic wave length and Stokes layer are small, and local body surface may be considered as a plane wall. Suppose the object oscillates around point o in Fig.5. Surface around point A oscillates nearly on its tangential direction, generating a vortical wave. Surface around point B oscillates nearly in its normal direction, mostly driving an acoustic wave. Most of the surface segments oscillate in oblique directions and drive both vortical and sound waves.

Vortical waves are only important in the Stokes layer with thickness [Eq(37)]. Waves outside the Stokes layer are irrotational/acoustical. Here we discuss a limiting case when is small compared with body dimension l and the sound wavelength , i.e.,

, . (47)

This is the mid range of frequency. Outside the Stokes layer, acoustic waves can be solved if boundary condition is set at the outside surface of the Stokes layer (shown in Fig.5 by dashed line), i.e., normal velocity at this surface. Since is very small, the boundary can approximately be set at the body surface, i.e.,

, (48)

where is the normal oscillating velocity on the object surface. Acoustic equations (12)&(13) with boundary condition (48) can be solved analytically or numerically.

In the local Cartesian coordinates (Fig.5), the vortical wave equation is:

. (49)

Suppose the tangential velocity from the acoustic solution at the object surface is . The tangential oscillating velocity at the body surface is . Then the boundary conditions for is:

, at ; (50)

, at .

The solution is:

. (51)

In summary, the solving procedures for the acoustic and vortical waves generated by an oscillating object with arbitrary shape in the frequency range (47) are:

(1)Acoustic solution with normal velocity of the body surface as the boundary condition;

(2)Analytical viscous solution in the inner field, Eq.(51), with tangential velocity (50) at the body surface.