ALTERNATIVE
PROJECTION
|
|
In contrast to Mercator projections, a flat-mapping technique called CARET (computerized anatomical, reconstruction and editing toolkit) preserves the area and length of objects, instead of their angles.
|
FLAT MAPS
OF THE BRAIN
|
A Mercator-like flat map of the brain can be viewed in three ways:
- Euclidean, which is flat like a road map. Distance is measured or scaled as expected.
- Hyperbolic, which is disk-shaped and allows the map focus to be changed so that the chosen center is in sharp focus and the edges distorted, much like moving a magnifying glass over a piece of paper.
- Spherical, which wraps a flattened brain image around a sphere.
|
|
. |
All those folds and fissures make life difficult for a neuroscientist: they bury two thirds of the brain's surface, or cortex, where most of the information processing takes place. With so much of the brain hidden, researchers have a hard time seeing exactly which parts of the cortex are doing what and how they are related to one another. "People want to see what's in the folds," says Monica K. Hurdal, a computer scientist at Florida State University, who has created a computer program to flat-map the brain. Conventional imaging techniques usually display cross sections of the brain, making it difficult to view the entire surface. For example, an MRI scan might show areas that look to be adjacent but are, if they have a deep fold between them, actually far apart.
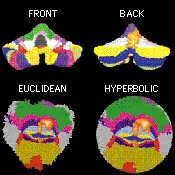 |
| CEREBELLUM'S FRONT AND BACK can be combined into single flat maps (shown here in Euclidean and hyperbolic views) to reveal details that are normally hidden in the brain's folds. |
"Converting a sphere into a plane is not so difficult," Hurdal explains, "but it does require that certain compromises be made." The Mercator projection of the earth, for instance, preserves shapes and angles at the expense of areas, so that the polar regions look far too large in relation to the equatorial ones. The mathematical basis for the Mercator projection is an 1851 law of geometry known as the Riemann mapping theorem (although the 16th-century cartographer himself wasn't aware of it, of course). It says that a three-dimensional curved surface can be flattened while preserving the angular information, thereby yielding a so-called conformal map.
To flatten the cortex, Hurdal takes anatomical information from a high-resolution, 3-D MRI scan and feeds it into her program. Within a few minutes, several algorithms convert the surface of the brain into a network of thousands or even millions of cortical points (the number depends on the size of the area to be flattened), each connected to its nearest neighbors by lines. The result is a triangulated mesh.
The key to flattening this landscape of convoluted triangles lies in a Greek theorem called circle packing. It says that three circles can always be drawn around the corners of a triangle so that each circle just touches the other two. Any two of these circles also belong to a neighboring triangle. Hence thousands of triangles in a flat plane can perfectly pack that plane with thousands of circles.
Applying the theorem to the brain may sound easy enough, but there is one problem, Hurdal notes: the triangles that represent the surface of a brain are not lying flat, so the touching circles will stick out. To fix this, the program employs a contemporary version of circle packing. It extends the theorem to three dimensions, moving all the cortical points until they settle down with the circles into a well-packed plane. Because the resulting maps are not perfect conformal maps, Hurdal calls them quasi-conformal. She has already flat-mapped the cerebellum and various bits of the cortex. To match precise regions with brain activity, researchers can take images from subsequent scans, flatten them and overlay them on the initial MRI.
Surgeons may eventually rely on the maps in brain surgery, particularly in epilepsy operations in which cutting out chunks of the cortex is necessary to help stop seizures. Werner K. Doyle, a neurosurgeon who performs more than 200 such operations every year at New York University--Mount Sinai Comprehensive Epilepsy Center, says, "Which parts are removed is often an educated guess."
The most commonly used method to locate malfunctioning regions is electroencephalography (EEG). It requires placing several electrodes directly on the surface of the brain and waiting for a seizure. Unfortunately, EEG readings don't always mark the right spot, and so too much cortex or the wrong region is sometimes removed. Flat maps turn the 3-D brain into a 2-D image, which, Doyle says, "will make it easier and safer for neurologists to navigate the mind." Ideally, no one will get lost, because directions aren't included.
Photo: COURTESY OF MONICA K. HURDAL
|


