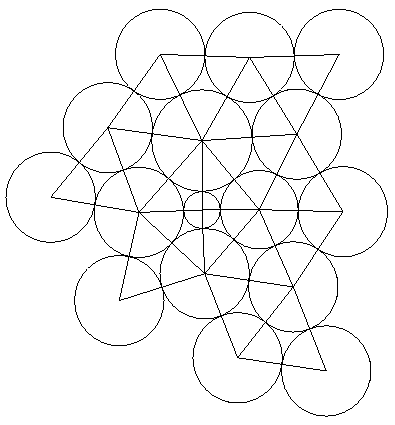This poster was presented as Poster #467 at the Sixth International Conference on Functional Mapping of the Human Mapping (HBM2000) held in San Antonio, Texas, U.S.A., June 12-16, 2000.

Abstracts for all posters are available online.

The abstract for this poster was published in NeuroImage, vol. 11, part 2, pg. S467, 2000.

COORDINATE SYSTEMS FOR CONFORMAL CEREBELLAR FLAT MAPS 1Monica K. Hurdal, 2Ken Stephenson, 1Philip L. Bowers, 1De Witt L. Sumners, 3,4David A. Rottenberg 1Department of Mathematics, Florida State University, Tallahassee, FL, U.S.A. 2Department of Mathematics, University of Tennessee, Knoxville, TN, U.S.A. 3PET Imaging Center, VA Medical Center, Minneapolis, MN, U.S.A. 4Departments of Neurology and Radiology, University of Minnesota, Minneapolis, MN, U.S.A. 1,2,3,4Members of the International Neuroimaging Consortium

Abstract we generate quasi-conformal Euclidean, hyperbolic and spherical flat maps of the human cerebellum via circle packings canonical surface-based coordinate systems can be imposed on these flat maps by specifying landmarks: 2 for hyperbolic coordinates, 3 for spherical coordinates We describe the use of anatomical landmarks for imposing canonical coordinate systems on cerebellar flat maps.

Surface Flattening it is impossible to flatten a curved 3D surface without introducing linear and areal distortion [1] the Riemann Mapping Theorem (1854) says it is possible to preserve conformal (angular) information: a surface can be flattened without introducing angular distortion [2] we generate quasi-conformal flat maps of the human cerebellum using circle packings [3, 4, 5]

Riemann Mapping Theorem (1854) If D is any simply-connected open set on a surface, with a distinguished point a an element of D and a specified direction (tangent vector) through a, then there is a UNIQUE conformal map (1-1 bijection) which takes D to the interior of the unit circle O in the plane, with a --> 0 and the specified direction point in the positive X direction [2]. **CONFORMAL MAPPINGS EXIST**

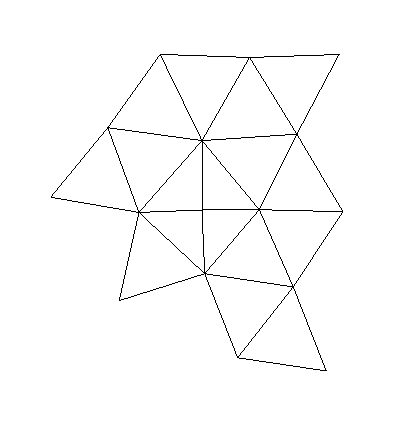
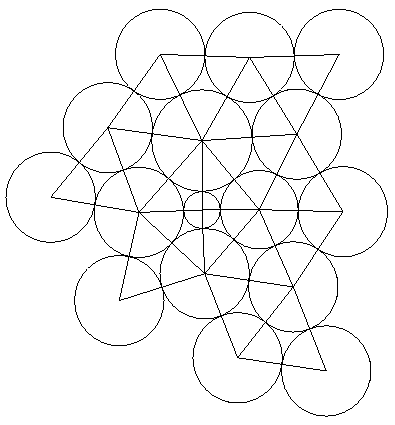
Circle Packings a configuration of circles with a specified pattern of tangencies is a circle packing a simple-connected planar triangulated surface can be represented with circles: each vertex is the center of a circle and if 2 vertices form an edge then their circles must be tangent to each other (Figure 1). Figure 1: A planar triangulation and its corresponding circle packing.

the Circle Packing Theorem and the Ring Lemma [6] guarantee that a there is a unique circle packing in the plane (up to certain transformations) which is quasi-conformal (bounded amount of angular distortion) for a simply-connected triangulated surface we have developed software [5, 7] which computes the circle packing of a simply-connected triangulated surface in 3D flat maps can be created in the conventional Euclidean plane, in the hyperbolic plane and on a sphere

Hyperbolic Flat Maps to our Euclidean eyes, portions of the hyperbolic map near the origin have little distortion and regions near the map border are greatly distorted (Figure 2) it is possible to move the focus of the hyperbolic map to change the regions which are in focus Figure 2: Planar representation of the hyperbolic plane [8]. Each devil is the same hyperbolic area. Since we look at this map with Euclidean eyes, regions near the boundary of the hyperbolic map appear greatly distorted.

Cerebellar Flat Maps interested in describing activated cerebellar foci in functional neuroimaging a high resolution T1-weighted MRI volume [9] was used to extract a cerebellar volume defined by a plane parallel to the posterior commisure-obex line and orthogonal to a plane passing through the vermal midline a topologically correct triangulated surface of the cerebellum was produced from this cerebellar volume

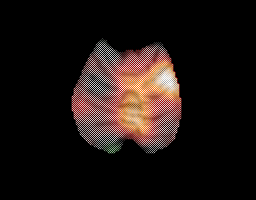
functional data obtained from a target interception experiment (Figure 3) various lobes and fissures color coded for identification purposes [10] (Figure 4) circle packing [7] was used to create quasi-conformal flat maps of the cerebellum (Figures 5, 6) 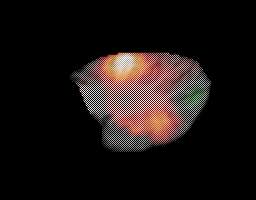Figure 3: Axial (left), coronal (middle) and sagittal (right) images showing PET functional activation of the cerebellum from a target interception task.

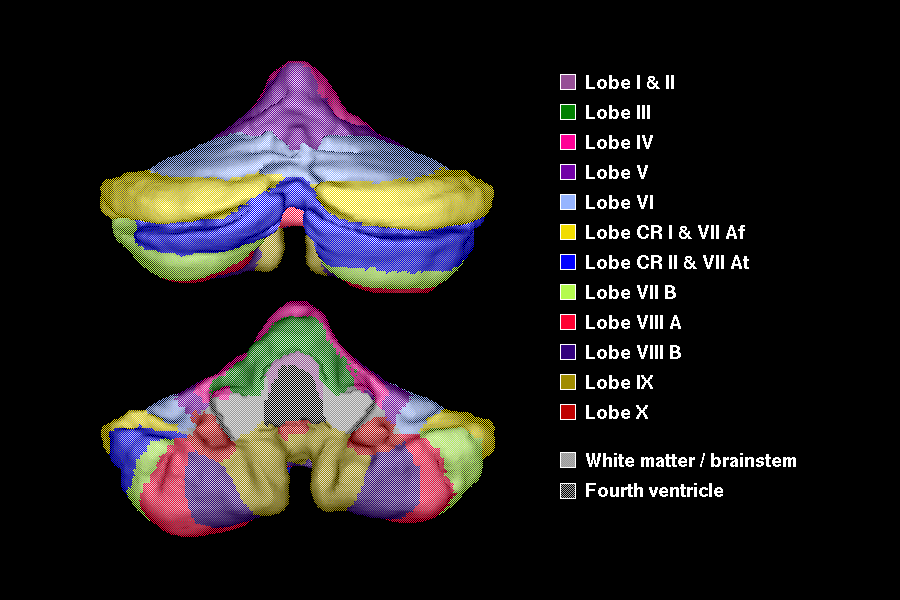
Figure 4: Surface of the cerebellum as viewed from the posterior (top) and anterior (bottom). The surface was colored according to the cerebellar atlas produced by [6].

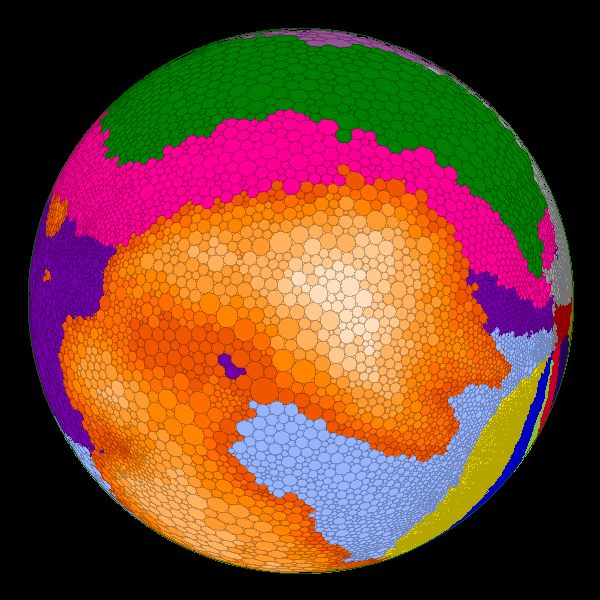
Figure 5: Quasi-conformal Euclidean flat map (left) and spherical map (right) of the cerebellum. The orange colors correspond to functional activation shown in Figure 3. Other colors correspond to regions shown in 4.

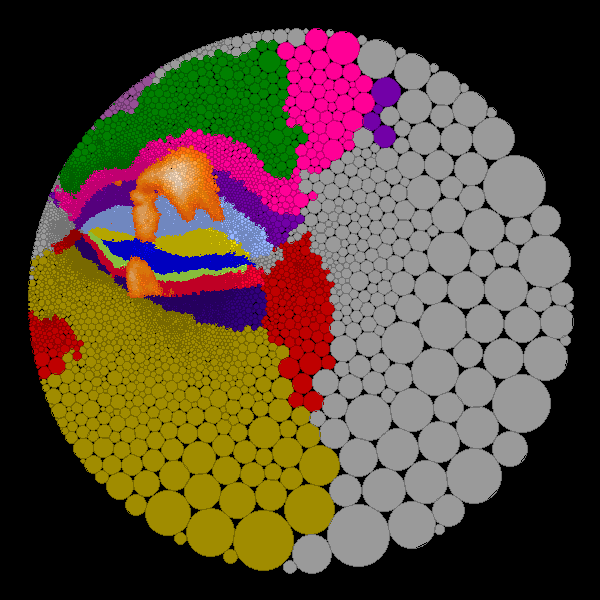
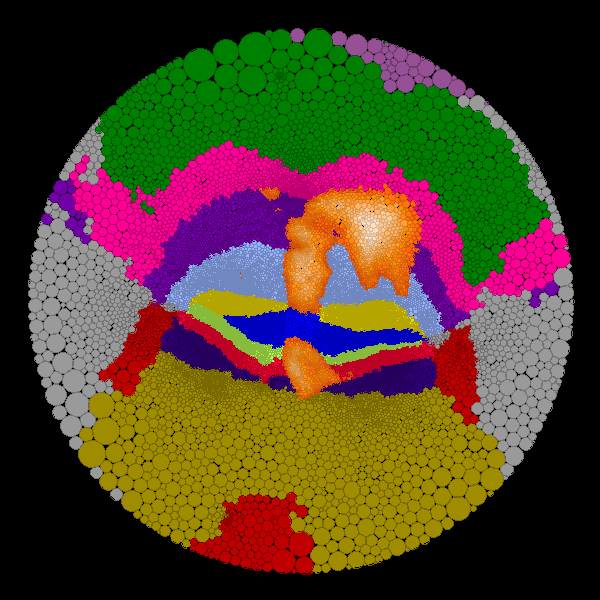
Figure 6: Quasi-conformal hyperbolic flat maps of the cerebellum. The orange colors correspond to functional activation shown in Figure 3. Other colors correspond to regions shown in Figure 4. The origin of the map can be altered to change the map focus to a region of interest. In this manner, regions of interest can be moved to the map center where there is little and other regions can be moved to map edges where distortion is higher.

A Canonical Coordinate System a canonical surface-based coordinate system can be imposed by specifying 2 points (such as anatomical or functional landmarks) on the hyperbolic map or 3 points on the spherical map [2, 11] 11 anatomical landmarks were identified (see poster on "Use of Cerebellar Landmarks ..." by Rehm et al.) we think flat maps with a canonical coord. system based on reproducible landmarks will improve functional localization

Hyperbolic Map Coordinate System two landmarks required for a canonical coordinate system: 1) midline base of horizontal fissure was used as the map center; 2) midline base of primary fissure was used to specify map orientation (i.e. positive y-axis) use a polar coordinate system (Figure 7, 8) map transformations are accomplished by Möbius transformations [11, 12]: f(z) = (a*z+b)/(c*z+d) where a,b,c,d are fixed complex numbers and a*d-b*c != 0

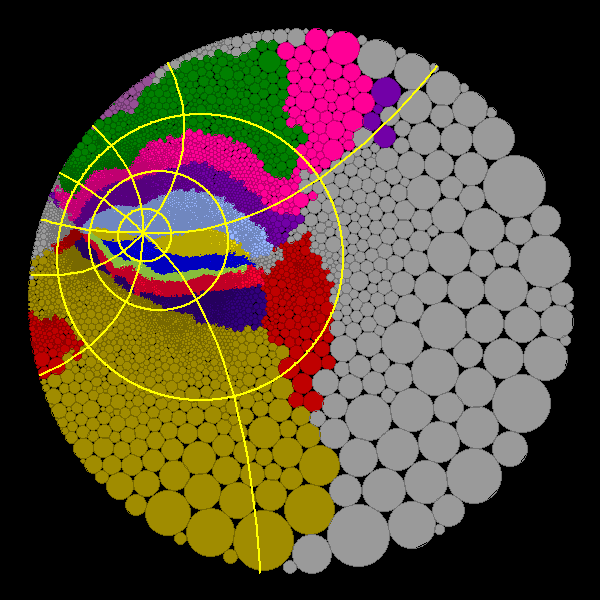
Figure 7: Two landmarks are required for a hyperbolic coordinate system. The figure on the right shows how the coordinate system is transformed when the map focus is changed. In this example, the coordinate system is merely transformed and not altered. Alternatively, a new coordinate system could be defined around the new map origin if desired.

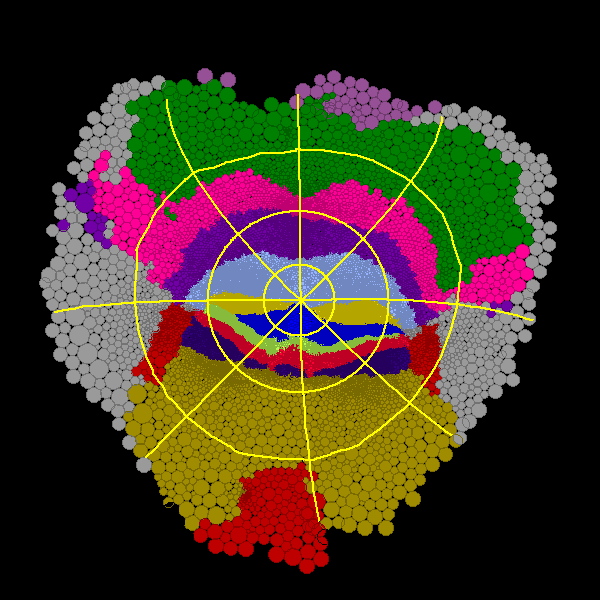
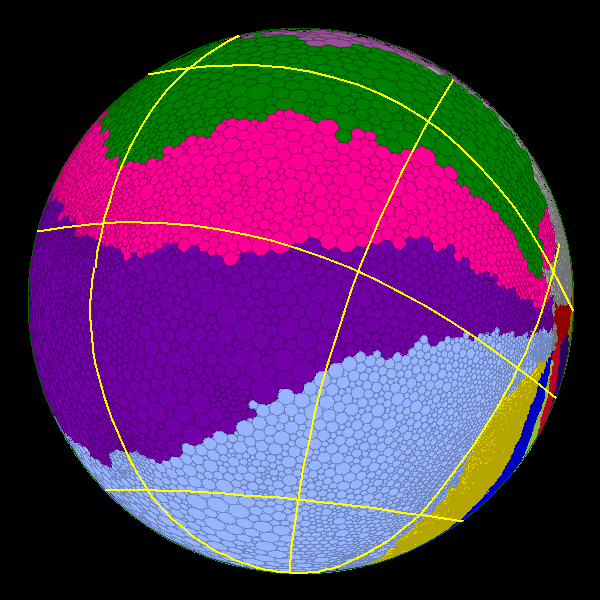
Figure 8: The coordinate lines from the hyperbolic map in Figure 7 as they appear on the Euclidean (left) and spherical maps (right).

Spherical Map Coordinate System three landmarks required for a canonical coordinate system: 1) midline base of precentral fissure was used as the north pole; 2) midline base of horizontal fissure was used as the south pole; 3) midline base of primary fissure was used as an equatorial point use a latitude and longitude coordinate system poles can be interactively changed to alter map distortion as with the hyperbolic maps

Advantages and Benefits conformal mappings preserve angle proportion and are mathematically unique a unique canonical surface coordinate system can be installed by choosing 2 points on a hyperbolic map or 3 points on a spherical map no extraneous cuts required on cortical surface to enhance flattening hyperbolic and spherical conformal maps allow the map focus and distortion to be transformed and changed

For more information... see our reprint: "Quasi-Conformally Flat Mapping the Human Cerebellum" in Lecture Notes in Computer Science, Springer-Verlag, Berlin, vol. 1679, pp. 279-286, 1999. contact: Dr. Monica K. Hurdal, Department of Mathematics, Florida State University, Tallahassee, FL., U.S.A., 32306-4510. Phone: (+1-850) 644-7378; Email: mhurdal@math.fsu.edu; WWW: http://www.math.fsu.edu/~mhurdal or visit the International Neuroimaging Consortium page ( http://pet.med.va.gov:8080/incweb/). This work has been supported in part by NIH grants MH57180 and NS33718. The authors would like to gratefully acknowledge Kelly Rehm, Kirt Schaper and Josh Stern, VA Medical Center, Minneapolis, U.S.A. for providing some of the data used in this presentation.

References [1] Polya, G., Mathematical Discovery, Volume 2, John Wiley & Sons, New York, 1968. [2] Ahlfors, L.V., Complex Analysis, McGraw-Hill Book Company, New York, 1996. [3] Hurdal, M.K., et al., Neuroimage, 1999, 9:S194. [4] Hurdal, M.K., et al., Lecture Notes in Computer Science, 1999, 1679:279-286. [5] See http://www.math.fsu.edu/~mhurdal for examples and information on software availability. [6] Rodin, B., Sullivan, D., J. Differential Geometry, 1987, 26:349-360. [7] Dubejko, T., Stephenson, K., Experimental Mathematics, 1995, 4:307-348. [8] Schattschneider, D., Visions of Symmetry, Notebooks, Periodic Drawings and Related Work of M.C. Escher, 1990. [9] Holmes, C.J., Hoge, R., Collins, L., Evans, A.C., Neuroimage, 1996, 3:S28. [10] Schmahmann, J.D., et al., Neuroimage, 1999, 10:233-260. [11] Beardon, A.F., The Geometry of Discrete Groups, Springer-Verlag, 1983. [12] Bedford, T., et al. (eds), Ergodic Theory, Symbolic Dynamics and Hyperbolic Spaces, Oxford University Press, New York, 1991.