This poster was presented as Poster #195 at the Fifth International
Conference on Functional Mapping of the Human Mapping
(HBM'99) held in Düsseldorf, Germany, June 22-26, 1999.
| |
|
|
|
|
| |
|
|
GENERATING CONFORMAL FLAT MAPS OF THE
CORTICAL SURFACE VIA
CIRCLE PACKING
1Monica K. Hurdal,
1De Witt L. Sumners,
2Ken Stephenson,
1Philip L. Bowers,
3,4David A. Rottenberg
 |
1Department of Mathematics,
Florida State University, Tallahassee, FL, U.S.A.
2Department of Mathematics, University of
Tennessee, Knoxville, TN, U.S.A.
3PET Imaging Center, VA Medical Center,
Minneapolis, MN, U.S.A.
4Department of Radiology, University of
Minnesota, Minneapolis, MN, U.S.A.
1,2,3,4Members of the International Neuroimaging
Consortium
|



|
|
|
| |
| |
|
|
|
| |
|
|
|
|
| |
|
|
Abstract
- a circle packing is a
configuration of circles with a specified pattern of tangencies
We present a novel method which uses circle packings to create flat maps of the cortical surface.
- these maps exhibit conformal behavior in that angular distortion is controlled
|
| |
| |
|
|
|
| |
|
|
|
|
| |
|
|
Surface Flattening
- it is impossible to flatten a curved 3D surface without introducing
linear and areal distortion [1]
- a surface can be flattened
without introducing angular distortion: a conformal
flat map [2]
- a piecewise flat bounded surface which is simply connected has no
holes and no handles (ie. a 2D disk)
- a triangulated representation of a cortical surface is topologically equivalent to a disk
|
| |
| |
|
|
|
| |
|
|
|
|
| |
|
|
Riemann Mapping
Theorem (1854)
If D is any simply-connected open set on a surface, with a
distignuished point a an element of D and a specified
direction (tangent vector)
through a, then there is a UNIQUE conformal
map (1-1 bijection) which takes D to the interior of
the unit circle O in the plane, with a --> 0 and the specified
direction point in the positive X direction [2]
(see Figure 1).
CONFORMAL MAPPINGS EXIST!
|
| |
| |
|
|
|
| |
|
|
|
|
| |
|
|
Circle Packing
- let K represent any simply-connected triangulated surface
- represent each vertex, v, of K by a circle
cv such that each vertex is located at the center of its
circle
- if vertices v and w are connected by an edge, then
the circles cv and cw are tangent
- assign a positive number to each boundary vertex
- this gives a circle
packing for K (see Figure 2)
|
| |
| |
|
|
|
| |
|
|
|
|
| |
|
|
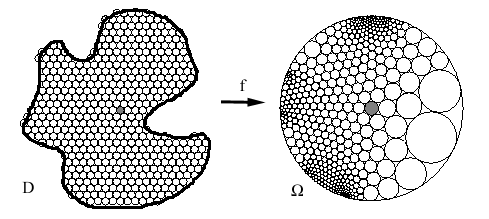
Figure 1: Example of a conformal map.
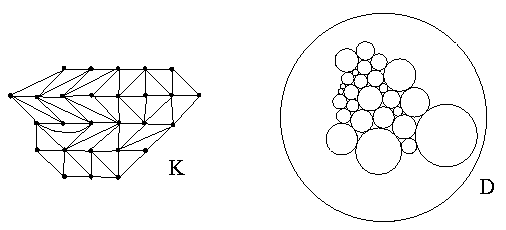
Figure 2: A triangulation (left figure) and its
resulting circle packing (right figure).
|
| |
| |
|
|
|
| |
|
|
|
|
| |
|
|
Circle Packing
Algorithm
- a new algorithm which
computes the circle packing of a simply connected triangulated surface
- result is an approximation to unique discrete conformal maps from a
3D cortical surface to the Euclidean plane, the hyperbolic plane or the
2-sphere
- to our Euclidean eyes, portions of the hyperbolic map near the
origin have little distortion and regions near the map border are greatly
distorted (Figure 3)
|
| |
| |
|
|
|
| |
|
|
|
|
| |
|
|
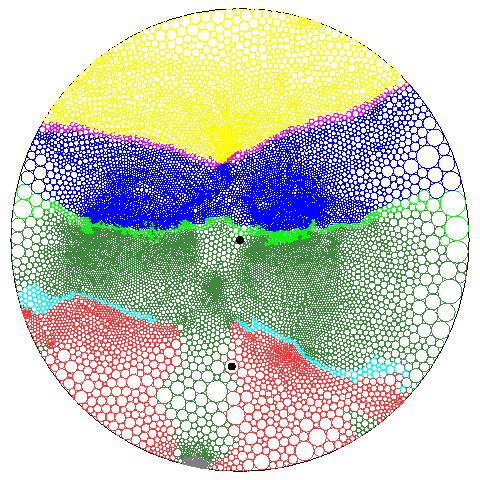
- it is possible to move the focus of the hyperbolic map to change
the regions which are in focus

Figure 3: Planar representation of the hyperbolic
plane [3]. Each devil is the same hyperbolic area. Since
we look at this map with Euclidean eyes, regions near the boundary of the
hyperbolic map appear greatly distorted.
|
| |
| |
|
|
|
| |
|
|
|
|
| |
|
|
- uniqueness of the conformal map is guaranteed by choosing 2 points
(ie. anatomical landmarks) or 1 point and a direction on the cortical
surface
- see Figures 4, 5 and
6 for examples of quasi-conformal flat maps created using
circle packing on data from the Macaque monkey
- see Poster #194 for examples of
quasi-conformal flat maps in the Euclidean plane, the hyperbolic plane and on a
sphere using data from the human cerebellum
|
| |
| |
|
|
|
| |
|
|
|
|
| |
|
|
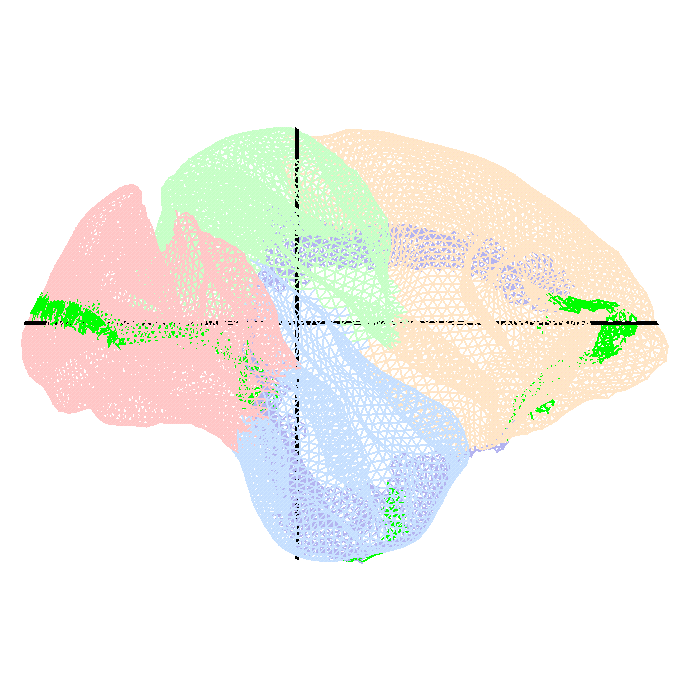
Figure 4: Triangulated surface representing the left
hemisphere of the Macaque monkey [4]. Colors correspond to
the following cortical regions: pink = occipital lobe; light green = parietal
lobe; blue = temporal lobe; orange = frontal lobe; purple = limbic cortex;
bright green = extra cuts introduced by Drury et al. [4]
to use as part of the boundary for flat maps.
|
| |
| |
|
|
|
| |
|
|
|
|
| |
|
|
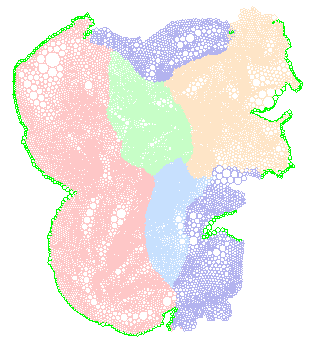
Figure 5: Quasi-conformal Euclidean flat map of
Macaque hemisphere. Colors correspond to regions shown in Figure
4.
|
| |
| |
|
|
|
| |
|
|
|
|
| |
|
|
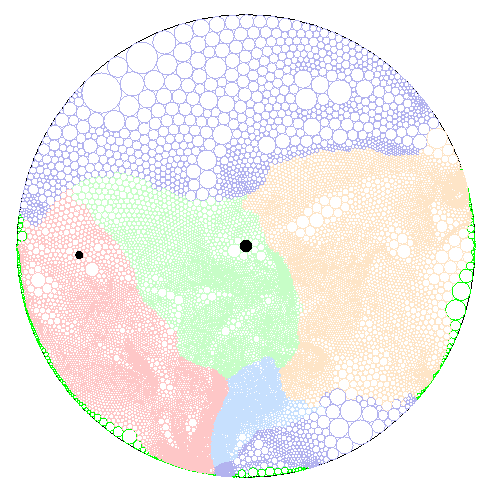
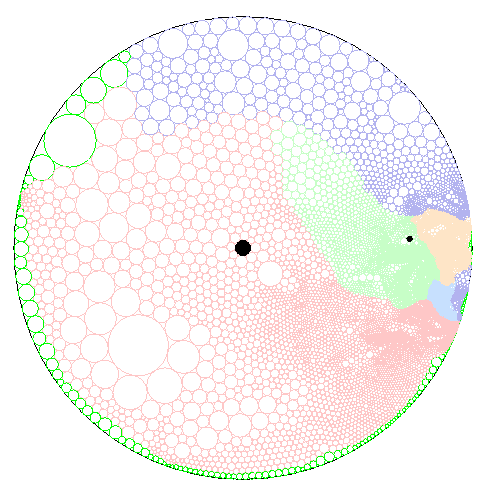
Figure 6: Quasi-conformal hyperbolic flat maps of the Macaque hemisphere. Colors correspond to regions shown in Figure
4. The origin (map focus) is marked in black in the center
of the maps. An alternate focus (marked in black on the left of the left map)
is used as the focus for the right map. The focus from the left map is marked
in black on the right side of the right map.
|
| |
| |
|
|
|
| |
|
|
|
|
| |
|
|
The Algorithm:
Case 1
- a piecewise flat surface composed of equilateral triangles, with
sides of length L
- each vertex, v, has the conditions described for a circle
packing
- each vertex, v, is represented in the plane by a circle,
cv, with radius L/2
- a vertex, v, belongs to k triangle faces, giving
k angles at v
- the angle sum,
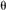 (v), is defined to be the sum of these
angles about v (v), is defined to be the sum of these
angles about v
|
| |
| |
|
|
|
| |
|
|
|
|
| |
|
|
- a set of circles can be "flattened" so they fit together in the
plane if
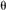 (v)
= 2 Pi (v)
= 2 Pi
- curvature is concentrated at the interior vertices
- to flatten the surface (see Figures 7 and
8)
- when
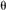 (v) < 2 Pi there is positive curvature (cone
point) which is represented by a gap between the circles around v, so
shrink the circles around v until all the circles around v are
tangent (v) < 2 Pi there is positive curvature (cone
point) which is represented by a gap between the circles around v, so
shrink the circles around v until all the circles around v are
tangent
- when
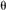 (v) = 2 Pi there is zero curvature and the map
is already flat at v (v) = 2 Pi there is zero curvature and the map
is already flat at v
|
| |
| |
|
|
|
| |
|
|
|
|
| |
|
|
- when
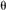 (v) > 2 Pi there is negative curvature (saddle
point) which is represented by overlapping circles in the plane, so expand
the circles around v until all circles around v are tangent (v) > 2 Pi there is negative curvature (saddle
point) which is represented by overlapping circles in the plane, so expand
the circles around v until all circles around v are tangent
- iteratively repeat this procedure at each vertex to obtain a
circle packing
- this circle packing is guaranteed to be
unique (up to certain transformations)
and quasi-conformal (bounded amount
of angular distortion) by the Circle Packing Theorem and the Ring Lemma
[5]
|
| |
| |
|
|
|
| |
|
|
|
|
| |
|
|
- denote t as the Euclidean measure of an angle at vertex
v in the 3D surface
- conformal flattening preserves the proportion of t in the
flattened surface
- the angular image of t has Euclidean measure
2*Pi*t/
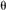 (v) (v)
- to reduce the angular distortion to zero refine the triangles in the
surface by subdividing each triangle into smaller triangles and repeat the
above procedure until the map converges to the unique conformal map
[6]
|
| |
| |
|
|
|
| |
|
|
|
|
| |
|
|
Figure 7: Example of how positive curvature (left) and
negative curvature (right) are represented in the plane and how the circles
need to be adjusted to achieve a circle packing (middle).
Figure 8: Example illustrating how a circle packing
(left) is iteratively adjusted (middle) to produce a quasi-conformal circle
packing (right).
|
| |
| |
|
|
|
| |
|
|
|
|
| |
|
|
The Algorithm:
Case 2
- surface triangulation is not equilateral
- modified circle packing algorithm where
- each vertex, v, is represented in the plane by a circle,
cv
- if vertices v and w are connected by an edge, then
the distance between circles cv and cw is
given by the inversive distance (a conformal invariant of circle pairs)
between v and w
- inversive distance rather than circle tangency is preserved
|
| |
| |
|
|
|
| |
|
|
|
|
| |
|
|
Advantages and
Benefits
- a conformal flat map is mathematically unique
- a unique conformal surface coordinate system can be installed on the
flat map by choosing 2 points or a point and a direction
- no cuts required on cortical surface to enhance flattening
- hyperbolic maps allow the map focus and distortion to be transformed
and changed
- minimal computation times on a 400MHz PII PC (minutes for the human
cerebellum)
|
| |
| |
|
|
|
|
|
| |
|
|
|
|
| |
|
|
References
[1] Polya, G., Mathematical Discovery, Volume 2,
John Wiley & Sons, New York, 1968.
[2] Ahlfors, L.V., Complex Analysis, McGraw-Hill
Book Company, New York, 1996.
[3] Schattschneider, D., Visions of Symmetry,
Notebooks, Periodic Drawings and Related Work of M.C. Esher, 1990.
[4] Drury, H. A., et al., J. Cog. Neurosci.,
1996, 8:1-28.
[5] Rodin, B., Sullivan, D., J. Differential
Geometery, 1987, 26:349-360.
[6] Bowers, P., Stephenson, K., Uniformizing
Dessins and Belyi Maps via CirclePacking, Submitted to Trans. A.M.S. and
available at
http://www.math.fsu.edu/~bowers |
| |
| |
|
|
|














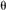 (v), is defined to be the sum of these
angles about v
(v), is defined to be the sum of these
angles about v