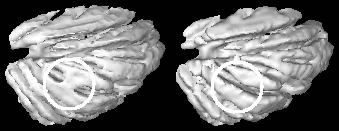
NeuroImage 13, Number 6, 2001, Part 2 of 2 Parts

METHODS - ACQUISITION

Automatic Surface Extraction by Discrete, Topologically Controlled,
Region Growing


Josh Stern, Kirt Schaper, Kelly Rehm, Monica Hurdal , De Witt Sumners,
David Rottenberg

Department of Neurology, University of Minnesota
PET Imaging Center, Minneapolis VA Medical Center
Department of Radiology, University of Minnesota
Department of Mathematics, Florida State University


Introduction:

Flat-mapping approaches [1,2,3] to anatomic visualization and functional modeling require polygonal surfaces that are topologically correct and topologically equivalent to a sphere (a single, closed, non-intersecting manifold with no exposed edges or handles) or a plane (like a sphere with a connected, non-looping set of polygons removed). The surfaces produced by the widely used Marching Cubes algorithm exhibit undersirable local topological defects, including surface holes, fins, and unconnected polygons. Alternative discrete algorithms for iso-surface extraction which do not produce topological defects have been proposed (c.f. [4]). However, these algorithms do not provide any mechanism for controlling topological genus. Deformable geometric models [5] can control topological genus and produce a correct surface, however their computational cost is much higher than the the discrete methods for any given level of spatial resolution, and the algorithms can very be sensitive to initialization conditions, choices of parameter values, and the appropriateness of their implicit anatomical models to their subject matter (e.g. the cerebellum may require different assumptions than the cortex). To avoid these issues, we have developed a discrete algorithm for producing topologically correct surfaces, at an arbitrary level of spatial granularity, which is fast and robust.

Method:

Our algorithm works by growing voxel regions and maintaining topology during the growing process. The core of the algorithm is indifferent to the particular topology to be maintained, but interesting neuroscientific applications focus on the sphere. The inputs to the algorithm are an initial guess about the region to be included within the volume and the desired sampling resolution for the region. The operatational stages of the algorithm are as follows: i) find the largest face-connected components of the region and fill its cavities; mask out all non-connected voxels; ii) label the within volume voxels by the length of the shortest face-connected path to non-volume voxels; iii) starting with a single voxel with the largest label (breaking ties arbitrarily) grow the region by iteratively adding to the region the face connected voxels with the largest score that do not change the topology, until voxels can no longer be added; iv) build a surface mesh from the outward facing exposed voxel faces; v) smooth the normals of the surface mesh for visual presentation. The actual implementation of the algorithm involves a large number of optimizations to insure that it is space efficient and scalable.

Figure: Cerebellar Surfaces extracted from T1 MRI prepared by Holmes et al. (1x1x1mm resolution). Marching Cubes Surface(left) has Euler characteristic of -256 and a handle spans a major fissure. Surface extracted by our algorithm has Euler characteristic 2, as expected.
Results:

The algorithm has been used extract surfaces with no topological defects that are topological spheres and have detail equivalent to surfaces produced by Marching Cubes (see figure). The running time to produce a surface with 50,000 vertices is about 10 minutes on a Pentium II 300 MHz machine.

References:

1. Van Essen D., et al. PNAS 95:788-795, 1998.
2. Dale A., et al. NeuroImage 9:179-194, 1999.
3. Hurdal M., et al. MICCAI'99: 279-286, 1999.
4. Montani C., et al. CompAidGeoDesgn 17: 207-232, 2000.
5. McInerney T., et al. MedImageAnal 1: 91-108, 1996.
6. Holmes C., et al. NeuroImage 3:S28, 1996.


This work was supported in part by NIH grant MH57180

S44