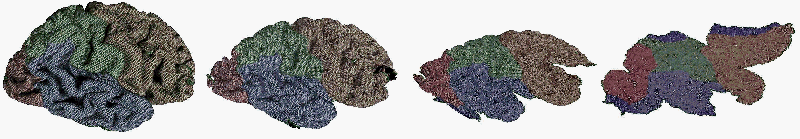9th International Conference on Human Brain Mapping, New York City, U.S.A., June 18-22, 2003
Visualization Tools for Interacting with Quasi-Conformal Flat Maps of the Human Brain
Kevin W. Kurtz , Monica K. Hurdal
, Monica K. Hurdal , David C. Banks
, David C. Banks
 Department of Computer Science and CSIT, Florida State University, Tallahassee, U.S.A.
Department of Computer Science and CSIT, Florida State University, Tallahassee, U.S.A.
 Department of Mathematics, Florida State University, Tallahassee, U.S.A.
Department of Mathematics, Florida State University, Tallahassee, U.S.A.
Abstract
A method for generating quasi-conformal maps using the method of Circle Packing
[1,2] has been adapted for cortical surface flattening [3]. Visualization
and computational tools are now needed to interact between cortical flat
maps and a 3D brain surface to gain information about spatial and functional
relationships that might not otherwise be apparent. Our group has developed
visualization and analysis tools that may help elucidate new information
about the human brain by interacting between a cortical surface and its corresponding
quasi-conformal flat map.
Methods
A topologically correct,
piecewise linear, triangulated mesh of a cortical surface is required for
flat mapping. We used the Circle Packing method to create quasi-conformal
flat maps of the right cerebral hemisphere. This approach yields a cortical
flat map composed of a collection of tangent circles, where the center of
each circle has a one-to-one correspondence to each vertex in the original
triangulated surface mesh. A single flat map is produced during the flattening
process with no intermediate maps. We have developed software tools using
Open Inventor to interactively morph between the original cortical surface
and the precomputed flat map. Linear interpolation is used to control the
morphing. A texture map of the circle packing flat map is imposed on the
original cortical surface and a bump mapped image of the flat map is also
generated to enhance navigation on the flat map. Tools we have developed
in X Windows allow the user to select a region of interest on the flat map,
display the corresponding region on the original 3D surface and calculate
the surface area for both regions.
Results
By imposing a
texture circle map onto the original cortical surface, the user can observe
circle deformations that occur when the circles from the circle packing flat
map are mapped back onto the original cortical surface. The user manipulates
a 3D widget within the program to control the morphing and linear interpolation
maps each circle to its final location in 3D based on the morphing variable.
Some frames from this process are illustrated in Fig. 1. Bump map coloring
assists the user with navigation on the flat map by revealing cortical folds
and fissures, while a user-selected region on the flat map and the corresponding
region can be computed on the 3D surface (Fig. 2).
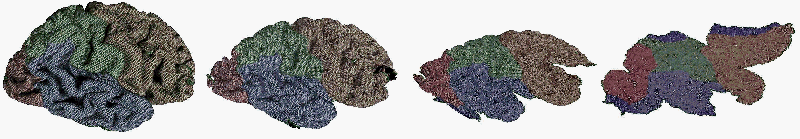 |
| Fig 1.: Morphing the cortical surface. |
 |
| Fig 2: Flat map; map with bump map texture; enlargement of selected region; selected region on 3D surface. |
Conclusions
Brain
atlases and cortical flat maps may assist researchers in making conclusions
regarding individual differences in functional organization of the human
brain. These visualization tools represent an initial attempt at being able
to interact with a cortical flat map and the corresponding cortical surface.
Such tools will contribute to a better understanding of the distortions that
can occur during flattening and improve the utility of cortical flat maps.
References
[1] Stephenson, K. 1999. Proceedings of the Third CMFT Conference 11:551-582.
[2] Collins, C.R. and K. Stephenson, K. To appear. Computational Geometry: Theory and Application.
[3] Hurdal, M.K. et al. 1999. Lecture Notes in Computer Science 1679:279-286.
Acknowledgments
This work is supported in part by NSF grants DMS-0101329 and 0083898, NIH grant MH57180 and FSU 2000 Planning grant.
NeuroImage, Volume 19, Number 2, Supplement 1, Page S45, CD-Rom Abstract 872, 2003
 , Monica K. Hurdal
, Monica K. Hurdal , David C. Banks
, David C. Banks
 Department of Computer Science and CSIT, Florida State University, Tallahassee, U.S.A.
Department of Computer Science and CSIT, Florida State University, Tallahassee, U.S.A. Department of Mathematics, Florida State University, Tallahassee, U.S.A.
Department of Mathematics, Florida State University, Tallahassee, U.S.A. , Monica K. Hurdal
, Monica K. Hurdal , David C. Banks
, David C. Banks
 Department of Computer Science and CSIT, Florida State University, Tallahassee, U.S.A.
Department of Computer Science and CSIT, Florida State University, Tallahassee, U.S.A. Department of Mathematics, Florida State University, Tallahassee, U.S.A.
Department of Mathematics, Florida State University, Tallahassee, U.S.A.