A Model for Characterizing Cortical Folding Patterns Across Species

1300 WTh-PM 

Monica Hurdal¹, Deborah Striegel¹

¹Department of Mathematics, Florida State University, Tallahassee, FL

Cortical folding patterns vary widely across species in terms of the number and location of folds. No consensus has been reached to explain cortical morphogenesis. Current hypotheses are mechanistic (Van Essen, 1997) and cellular (Noctor et al., 2004). We adopt the intermediate progenitor (IP) model hypothesis (Kriegstein et al., 2006) and present a mathematical model to offer a possible explanation as to the location of cortical fold formation.

During cortical development, a proliferative layer of cells lines the lateral ventricle (LV), called the ventricular zone (VZ). Radial glial cells in the VZ are activated to create subsets of IP cells which create a local neuron amplification, resulting in gyrus formation. We use a Turing reaction-diffusion system (Turing, 1957) to model cortical folding pattern formation. This model offers an explanation as to why certain species may have little or no folding and it is able to predict the consistency in pattern formation across species.

Turing systems have been used to study pattern formation in many biological applications, including bacteria (Varea et al., 1999) and animal coat patterns (Murray, 2003). A Turing system is a reaction-diffusion system of two chemical morphogens representing an activator and an inhibitor. The biological basis of our model is that chemical morphogens may be governed by specific genes to regulate IP cell production. The LV and the VZ are key components in the IP model hypothesis of cortical pattern formation. We model the shape of the LV with a prolate spheroid and the VZ with a prolate spheroidal surface. The major axis of the prolate spheroid corresponds to the major axis of the lateral ventricle (Striegel and Hurdal, 2009). The focal distance of the prolate spheroid models the eccentricity of the LV. We discretized the Turing system and used periodic boundary conditions to carry out numerical simulations to study the role of domain scaling on the arising pattern.

We have developed a formula that enables pattern formation to be predicted on a prolate spheroid domain by relating a given domain scale and domain shape to the arising pattern. This pattern is indicated by the spheroidal indices (m,n). Given a two tone color gradient such as black to copper, m corresponds to the number of copper (or black) spots traversing φ (where φ is the rotation term of the prolate spheroid) and n corresponds to m plus the number of shifts from copper to black (or black to copper) traversing θ (where θ is the asymptotic angle with respect to the prolate spheroid major axis) for a fixed φ. 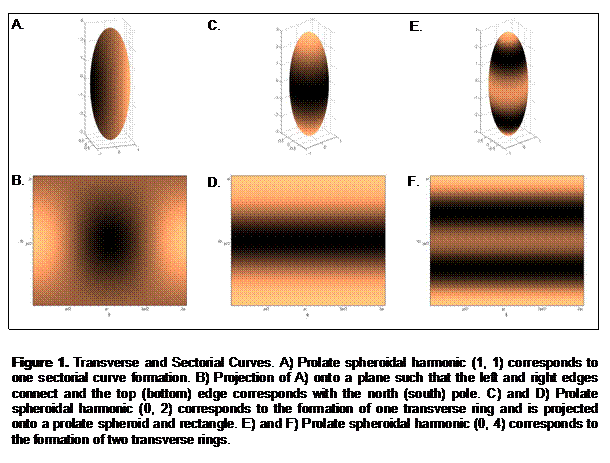Copper regions can be considered to be activated regions and black regions are non-activated regions. Sectorial curves are formed when the spheroidal harmonic indices are equal. For example (m,n) = (1,1) forms one sectorial curve, (2,2) forms two sectorial curves, etc. Transverse curves are formed for spheroidal harmonic indices (0,n) for n even. For example, (0,2) forms one transverse curve, (0,4) forms two transverse curves, etc. Examples of transverse and sectorial curves are shown in Figure 1.

Prolate spheroidal harmonics may be characterized in terms of cortical sulci. Sectorial sulci in the brain correspond to sulci that extend from the frontal lobe around the Sylvian fissure to the temporal lobe, matching the direction of the major axis of the prolate spheroid approximating the LV. Examples include the calcarine and cingulate sulci. Transverse sulci correspond to rings around the VZ. Examples include the central and precentral sulci.

Our simulations revealed that increasing the focal distance changed the order in which transverse and sectorial curves formed. For smaller focal distances, a sectorial curve is formed first. As focal distance increases, then as the domain scaling increases a transverse curve forms before the first sectorial curve. Greater increases in focal distance result in two transverse curves forming before a sectorial curve.

Our model illustrates how sulcal placement and directionality are related to changes in focal distance. We observed that as focal distance increased, the order of transverse and sectorial curves changed. Thus, focal distance affects the order in which curves, and hence sulci, are formed. One interpretation of these results relates to evolution. Earlier in an evolutionary timeline when the LV focal distances are smaller, the first transverse sulcus appears. Later when the focal distances are larger, a second transverse sulcus appears. Many species exhibit these sulcal formation patterns. Thus, we are able to predict cortical patterns that correlate with cortical observations. Our model is able to capture global shape characteristics of the cortex and it can link the evolutionary development of cortical sulcal formation to the eccentricity of the lateral ventricle. This model represents an important step in improving our understanding of cortical folding pattern formation of the brain.

Kriegstein, A. (2006), 'Patterns of Neural Stem and Progenitor Cell Division may Underlie Evolutionary Cortical Expansion', Nat Rev Neurosci, vol. 7, pp. 883-890.
Murray, J.D. (2003), Mathematical Biology II: Spatial Models and Biomedical Applications.
Noctor, S.C. (2004), 'Cortical Neurons Arise in Symmetric and Asymmetric Division Zones and Migrate through Specific Phases', Nat Neurosci, vol. 7, pp. 136-144.
Striegel, D.A. (2009), 'Chemically Based Mathematical Model for Development of Cerebral Cortical Folding Patterns', PLoS Comput Biol, vol. 5, pp. e1000524.
Turing, A.M. (1957), 'The Chemical Basis of Morphogenesis', Philos T R Soc Lond, B, vol. 237, pp. 37-72.
Van Essen, D.C. (1997), 'A Tension-based Theory of Morphogenesis and Compact Wiring in the Central Nervous System', Nature, vol. 385, pp. 313-318.
Varea, C. (1999), 'Turing Patterns on a Sphere', Phys Rev E, vol. 60, pp. 4588-4592.