NeuroImage 9, Number 6, 1999, Part 2 of 2 Parts
METHODS, PHYSIOLOGY, COGNITION
Generating Conformal Flat Maps of the Cortical Surface via Circle Packing
Monica K. Hurdal ,
De Witt L. Sumners
,
De Witt L. Sumners ,
Ken Stephenson
,
Ken Stephenson ,
,
Philip L. Bowers ,
David A. Rottenberg
,
David A. Rottenberg
 Department of Mathematics, Florida State University, Tallahassee, U.S.A.
Department of Mathematics, Florida State University, Tallahassee, U.S.A.
 Department of Mathematics, University of Tennessee, Knoxvillee, U.S.A.
Department of Mathematics, University of Tennessee, Knoxvillee, U.S.A.
 PET Imaging Center, VA Medical Center, Minneapolis, U.S.A.
PET Imaging Center, VA Medical Center, Minneapolis, U.S.A.
 Department of Radiology, University of Minnesota, Minneapolis, U.S.A.
Department of Radiology, University of Minnesota, Minneapolis, U.S.A.
Abstract. A circle packing is a configuration of circles
with a specified pattern of tangencies. We present a novel method which uses
circle packing to create flat maps of the cortical surface. These maps exhibit
conformal behavior in that angular distortion is controlled.
Methods. Let K represent a simply-connected triangulated
surface which is a 2-manifold. Then there exists a circle packing for K
on the Riemann sphere. This circle packing is unique up to Möbius
transformations and inversions of the Riemann sphere. Furthermore, this
packing represents a discrete conformal map (1). A packing for K is
created as follows. Each vertex, v, of K is represented by a
circle cv with the center of cv located
at v. If vertices v and w are connected by an edge, then
the circles cv and cw are tangent.
Vertex v belongs to k triangle faces, giving k
angles at v. The sum of these angles is defined to be the angle sum
of v, 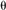 (v).
A set of circles can be "flattened" so they fit together in the plane if
(v).
A set of circles can be "flattened" so they fit together in the plane if
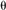 (v) = 2Pi. This
is accomplished by iteratively refining the circle packing and adjusting each
angle at v. This process is repeated for all interior vertices until a
nominated accuracy in the angle sums is achieved (2).
(v) = 2Pi. This
is accomplished by iteratively refining the circle packing and adjusting each
angle at v. This process is repeated for all interior vertices until a
nominated accuracy in the angle sums is achieved (2).
Results and Conclusions. This is a novel method that seeks to
preserve conformal information and produce, as a first approximation, a flat
quasi-conformal mapping of the 2D piecewise cortical surface in the
conventional Euclidean plane. No cuts in the original cortical surface are
required. This mapping can also be created in the hyperbolic plane which
allows the map origin to be transformed interactively so that different
anatomical landmarks can be used as the map focus. Color can be used to
identify anatomical features. Results obtained from this approach which use
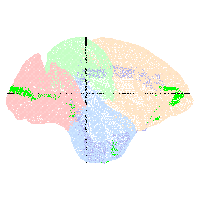
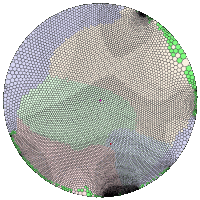
triangulated macaque (3) and human cortical surfaces are presented.
 |
 |
 |
| Reconstruction of Macaque
Cortex (3) |
Hyperbolic Flat Map |
Hyperbolic Map with Different Map
Origin |
1. Dubejko, T., Stephenson, K., Experimental Mathematics, 1995, 4:307-348.
2. Stephenson, K., Computation Methods in Function Theory, 1997, "The
Approximation of Conformal Structures via Circle Packing", Available at URL
http://www.math.utk.edu/~kens
3. Drury, H. A, Van Essen, D. C., Anderson, C. H., Lee, C. W.,
Coogan, T. A., Lewis, J. W., 1996, J. Cog. Neurosci., 8:1-28.
Acknowledgments. The authors would like to gratefully
acknowledge Heather Drury and David Van Essen from Washington University
Medical School, St. Louis, U.S.A., for their kind assistance in providing
some of the data used in this presentation. This work has been
supported in part by NIH grants MH57180 and NS33718.
S195
 ,
De Witt L. Sumners
,
De Witt L. Sumners ,
Ken Stephenson
,
Ken Stephenson ,
, ,
David A. Rottenberg
,
David A. Rottenberg
 Department of Mathematics, Florida State University, Tallahassee, U.S.A.
Department of Mathematics, Florida State University, Tallahassee, U.S.A.
 Department of Mathematics, University of Tennessee, Knoxvillee, U.S.A.
Department of Mathematics, University of Tennessee, Knoxvillee, U.S.A.
 PET Imaging Center, VA Medical Center, Minneapolis, U.S.A.
PET Imaging Center, VA Medical Center, Minneapolis, U.S.A.
 Department of Radiology, University of Minnesota, Minneapolis, U.S.A.
Department of Radiology, University of Minnesota, Minneapolis, U.S.A.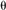 (v).
A set of circles can be "flattened" so they fit together in the plane if
(v).
A set of circles can be "flattened" so they fit together in the plane if


