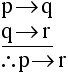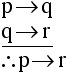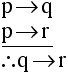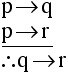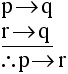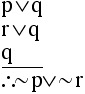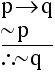
Unit 2 Module 1
Arguments and patterns of reasoning
An argument is formed when we try to connect bits of evidence (premises) in a way that will force the audience to draw a desired conclusion.
Consider these two arguments, such as a prosecutor might present to a jury:
1. The person who robbed the Mini-Mart drives a 1989 Toyota Tercel.
Gomer drives a 1989 Toyota Tercel. Therefore, Gomer robbed the Mini-Mart.
2. The person who drank my coffee left this fingerprint on the cup.
Gomer is the only person in the world who has this fingerprint.
Therefore, Gomer is the person who drank my coffee.
One of these arguments is convincing, and one is not. Why?
1. The person who robbed the Mini-Mart drives a 1989 Toyota Tercel. Gomer drives a 1989 Toyota Tercel. Therefore, Gomer robbed the Mini-Mart.
Evidence (premises):
A. The person who robbed the Mini-Mart drives a 1989 Toyota Tercel.
B. Gomer drives a 1989 Toyota Tercel.
Desired conclusion:
Therefore, Gomer robbed the Mini-Mart.
2. The person who drank my coffee left this fingerprint on the cup. Gomer is the only person in the world who has this fingerprint. Therefore, Gomer is the person who drank my coffee.
Evidence (premises):
A. The person who drank my coffee left this fingerprint on the cup.
B. Gomer is the only person in the world who has this fingerprint.
Desired conclusion:
Therefore, Gomer is the person who drank my coffee.
VALID ARGUMENTS
In a well-formulated argument, it should be logically impossible to reject the conclusion if we accept all of the evidence ("the truth of the premises forces the conclusion to be true;" or "the conclusion is an inescapable consequence of the premises").
Such an argument is called VALID.
On the other hand:
INVALID ARGUMENTS
An argument is poorly-formed if it is logically possible for the audience to believe all of the evidence and yet reject the conclusion.
More formally:
An argument is said to be INVALID if it is logically possible for the CONCLUSION to be FALSE even though EVERY PREMISE is assumed to be TRUE.
The preceding statement may be referred to as the Fundamental Principle of Argumentation. It governs our entire discussion of arguments and reasoning.
Notice that in the first argument given above, even if the jury believes all of the evidence, they don't necessarily have to believe the conclusion (because there are many people besides Gomer who drive 1989 Toyota Tercels). That is what makes the first argument invalid.
Notice that in the second argument, however, if the jury believes all of the evidence, then they must accept the conclusion. That is what makes the second argument valid.
Based on the Fundamental Principle of Argumentation, we have the following procedure that can be used to analyze arguments whose statements can be symbolized with logical connectives:
Technique for using truth tables to analyze arguments
1. Symbolize (consistently) all of the premises and the conclusion.
2. Make a truth table having a column for each premise and for the conclusion.
3. If there is a row in the truth table where every premise column is true but the conclusion column is false (a bad row) then the argument is invalid. If there are no bad rows, then the argument is valid.
Note: this technique is a simplified version of the method presented in section 2.6 of Mathematical Ideas.
EXAMPLE 2.1.1
Use a truth table to test the validity of the following argument.
If the apartment is damaged, then the deposit won't be refunded.
The apartment isn't damaged.
Therefore, the deposit will be refunded.
EXAMPLE 2.1.1 Solution
Step 1: Symbolize the argument.
Let p be the statement "The apartment is damaged."
Let q be the statement "The deposit won't be refunded."
Then the argument has this form:
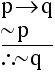
Note: the triangular configuration of dots represents the word "therefore."
Step 2: Make a truth table having a column for each premise and for the conclusion.
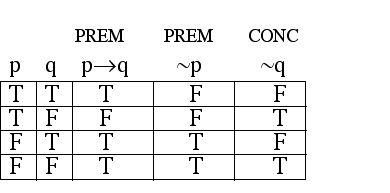
Step 3: Look for the indication of an INVALID argument (a row where every premise is true while the conclusion is false).
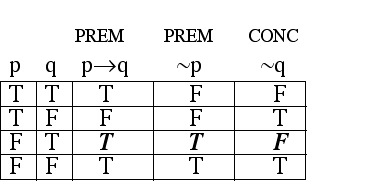
Notice that in the third row, both premises are true while the conclusion is false; this "bad row" tells us that the argument is INVALID.
EXAMPLE 2.1.2
Use a truth table to test the validity of this argument.
If I had a hammer, I would hammer in the morning.
I don't hammer in the morning.
Therefore, I don't have a hammer.
EXAMPLE 2.1.2 Solution
Step 1: Symbolize the argument.
Let p be the statement "I have a hammer."
Let q be the statement "I hammer in the morning."
Then the argument has this form:
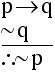
Note: the triangular configuration of dots represents the word "therefore."
Step 2: Make a truth table having a column for each premise and for the conclusion.
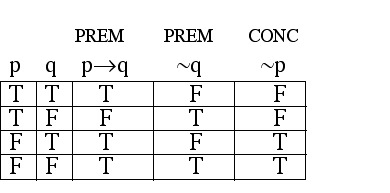
Step 3: Look for the indication of an INVALID argument (a row where every premise is true while the conclusion is false).
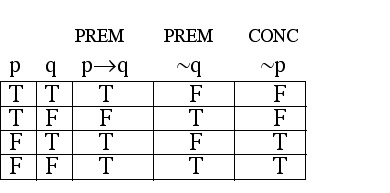
Notice that there is no row where the conclusion column is false while both premise columns are true; the absence of a "bad row" tells us that the argument is VALID.
Common patterns of reasoning: Contrapositive Reasoning
From the result in EXAMPLE 2.1.2 we have the following general fact
Any argument that can be reduced to the form
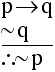
will be a valid argument.
This is a common form of valid reasoning known as Contrapositive Reasoning or Modus Tollens.
Example 2.1.3
Without making a truth table,
we know automatically that this is a valid argument:
If it rains, then I won't go out.
I went out.
Therefore, it didn't rain.
Here is another example of Contrapositive Reasoning (in set language):
All cats have rodent breath.
Whiskers doesn't have rodent breath.
Thus, Whiskers isn't a cat.
Note: the previous argument agrees with the form Contrapositive Reasoning because it can be rephrased in "if...then" language:
If one is a cat, then one has rodent breath.
Whiskers doesn't have rodent breath.
Therefore, Whiskers isn't a cat
(where the individual "Whiskers" is taking the place of
the general subject "one..." in the first premise).
Common patterns of reasoning (Fallacy of the Inverse)
Generalizing from the result of Example 2.1.1 above, we see that any argument that can be reduced to the form
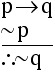
will be an invalid argument.
This is a common form of invalid reasoning known as Fallacy of the Inverse.
Example 2.1.4
Without having to make a truth table, we automatically know that the
following argument is INVALID:
If you drink Pepsi, then you are happy.
You don't drink Pepsi.
Therefore, you aren't happy.
Here is another example of Fallacy of the Inverse
(in set language):
All firefighters are courageous.
Gomer the Bold isn't a firefighter.
Thus, Gomer the Bold isn't courageous.
EXAMPLE 2.1.5
"There's a fine line between clever and stupid."
Nigel Tufnel, lead guitarist, Spinal Tap
Can you discern the "fine line between clever and stupid" in these two arguments?
Argument 1:
If I get a huge tax refund, then I'll buy a Yugo. I didn't buy a Yugo.
Therefore, I didn't get a huge tax refund.
Argument 2:
If I get a huge tax refund,
then I'll buy a Yugo. I didn't get a huge tax refund.
Therefore, I didn't buy a Yugo.
EXAMPLE 2.1.5 Solution
Argument 1 is VALID (it is Contrapositive Reasoning),
whereas Argument 2 is INVALID (it is Fallacy of the Inverse).
EXAMPLE 2.1.6
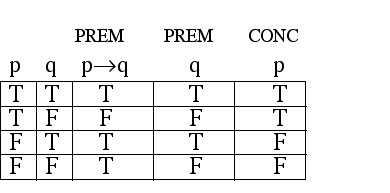
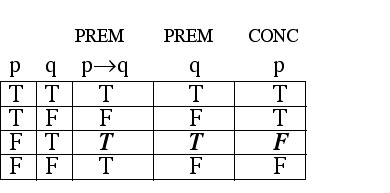
Use a truth table to test
the validity of this argument.
If one grows vegetables, then one is a gardener.
Gomer is a gardener.
Therefore, Gomer grows vegetables.
EXAMPLE 2.1.6 Solution Then the argument has this form: (Notice that "Gomer"
is taking the place of the more general subject "One..." in the first premise.)
Step 2: Make a truth table having a column for each premise
and for the conclusion.
Step 3: Look for the indication of an INVALID
argument (a row where every premise is true while the conclusion is false). Notice that in the third row, both premises are true while the conclusion is false; this "bad row" tells us that the argument is INVALID.
Common patterns of reasoning: Fallacy of the Converse Any argument that can be reduced to the form This is a common form of invalid reasoning known
as Fallacy of the Converse.
EXAMPLE 2.1.7 Test the validity of the following arguments. All great writers are philosophical. Thoreau was philosphical.
EXAMPLE 2.1.7 Solution Both arguments are INVALID, because they are examples of Fallacy of the Converse. It is not necessary to make the truth tables, although the truth tables will verify the claims that these areguments are invalid.
EXAMPLE 2.1.8 Test the validity of this argument (from Aristotle):
EXAMPLE 2.1.8 SOLUTION "If (subject) is a man, then (subject) is mortal." We symbolize the statements. If we employ the truth table technique to analyze this argument, we will see that it is VALID.
Common patterns of reasoning (Direct Reasoning) Any argument that can be reduced to the
form This common form of valid reasoning is called Direct Reasoning or Modus Ponens. Although we have not made a truth table to verify the claim that this is a form of valid reasoning, the fact is that if we make a truth table having a column for both premises and for the conclusion, these will be no "bad row."
Examples The following arguments are automatically
valid (because they are examples of Direct Reasoning):
If I quit school, I'll sell apples on the corner.
In set language: All Gators are obnoxious.
EXAMPLES No beggars are choosers.
Note: This last argument conforms to the pattern of Direct Reasoning
because the statement "No beggars are choosers" can be rephrased as "If one is a beggar,
then one isn't a chooser."
EXAMPLES Test the validity of each argument. SOLUTIONS 1. Valid 2. Invalid 3. Invalid 4. Valid
EXAMPLE 2.1.8 Test the validity of this argument: I have my keys or I'm locked out.
EXAMPLE 2.1.8 Solution Step 1: Symbolize the argument. Let p be the statement "I have my keys." Then the argument has this form: Step 2: Make a truth table having a column for each premise and for the conclusion. Step 3: Look for the indication of an INVALID argument (a row where every premise is true while the conclusion is false). Notice that there is no row in which the conclusion is false while both premises are true. The absence of such a "bad row" indicates that this argument is VALID.
Common patterns of reasoning (Disjunctive Syllogism) Any argument that can be reduced to the form This is a common form of valid reasoning known as disjunctive syllogism. Note: because the "or" connective is symmetric, this pattern can also be written as
Example This argument is automatically valid:
EXAMPLE 2.1.9 Test the validity of this argument: I walk or I chew gum.
EXAMPLE 2.1.9 SOLUTION First, symbolize the argument. Let p be the statement "I walk." Then the argument has this symbolic form: Notice that although this form looks similar to Disjunctive Syllogism,
it is significantly different in the second premise and conclusion.
Since this form doesn't conform to any of the common patterns that we have
encountered so far, we must use a truth table. Since in the first row we have both premises true while the conclusion is false, we see that this argument is INVALID.
Common patterns of reasoning (Disjunctive Fallacy) Any argument that can be reduced to one of these forms: This incorrect attempt to use the disjunctive syllogism is called DISJUNCTIVE FALLACY.
EXAMPLES The following arguments are INVALID, because they are examples of Disjunctive Fallacy; Today isn't Sunday or I can stay home. I can stay home. Therefore, today is Sunday. Fido is a poodle or has brown fur. Fido is a poodle. Therefore, Fido doesn't have brown fur.
For lots of practice in the art of using truth tables to analyze arguments, try: Test the validity of this argument: If I get elected, I'll reduce taxes. If I reduce taxes, the economy will prosper. Thus, if I get elected, the economy will prosper. EXAMPLE 2.1.10 Solution Let p be the statement "I get elected." Let q be the statement "I reduce taxes." Let r be the statement "The economy will prosper." The argument has this symbolic form: If you make a truth table having a column for each premise and a column for the conclusion, you will see that the argument is VALID. Common patterns of reasoning TRANSITIVE REASONING Any argument that can be reduced to the form is VALID. This is a common form of valid reasoning known as Transitive Reasoning. EXAMPLES: The following arguments are valid because they are examples of Transitive Reasoning. If today is Monday, then tomorrow is Tuesday. If tomorrow is Tuesday, then the day after tomorrow is Wednesday. Therefore, if today is Monday, then the day after tomorrow is Wednesday. In set language: All bulldogs are mean-looking dogs. All mean-looking dogs are good watchdogs. Therefore, all bulldogs are good watchdogs. Another example: If I eat my spinach, then I'll become well-muscled. If I become well-muscled, then I'll become a professional wrestler. If I become I professional wrestler, then I'll bleach my hair. If I bleach my hair, then I'll wear sequined tights. If I wear sequined tights, then I'll be ridiculous. Therefore, if I eat my spinach, then I'll be ridiculous. The previous example illustrates an important property of Transitive Reasoning: This method of reasoning extends indefinitely. We easily can construct valid arguments that have as many "if...then" premises as we wish, as long as the fundamental pattern continues: namely, the antecedent of each new premise agrees with the consequent of the previous premise. EXAMPLE 2.1.11 Test the validity of this argument: If I get elected, I'll take lots of bribes. If I get elected, I'll reduce taxes. Thus, if I take lots of bribes, then I'll reduce taxes. EXAMPLE 2.1.11 Solution Let p be the statement "I get elected." Let q be the statement "I take lots of bribes." Let r be the statement "I reduce taxes." The argument as this symbolic form: Notice that although this form looks somewhat similar to Transitive Reasoning, in fact it is significantly different from Transitive Reasoning in the second premise and the conclusion. In fact, a truth table will show you that this argument is INVALID. Common patterns of reasoning FALSE CHAINS Any argument that can be reduced to one of these forms will be invalid. These common forms of invalid reasoning are called False Chains. The following arguments are INVALID because they are examples of False Chains. If today is a state holiday, then school is closed. If today is Sunday, then school is closed. Therefore, if today is a state holiday, then today is Sunday. All cats are mammals. All cats are predators. Therefore, all mammals are predators. ARGUMENTS THAT DON'T CONFORM TO COMMON PATTERNS Common patterns of reasoning are useful in that they allow us to analyze arguments without having to construct truth tables. Of course, not every argument will conform to one of those patterns. EXAMPLE 2.1.12 Test the validity of the following argument: You have jumper cables or our date is cancelled. You have a credit card or our date is cancelled. Our date is cancelled. Therefore, you don't have jumper cables or you don't have a credit card. A. Valid B. Invalid EXAMPLE 2.1.12 SOLUTION We start by symbolizing the argument. Let p be the statement "You have jumper cables." Let q be the statement "Our date is cancelled." Let r be the statement "You have a credit card." The argument has this symbolic form: Now we make a truth table having a column for each premise and for the conclusion. Notice that in the first row, every premise is true while the conclusion is false. This indicates that the argument is INVALID. EXAMPLE 2.1.13 Test the validity of this argument: I got a scholarship and I got an "A" in math. I'm not good at logic or I got an "A" in math. Therefore, I'm good at logic or I don't get a scholarship. A. Valid B. Invalid EXAMPLE 2.1.14 Test the validity of the following argument. If I want to be a lawyer, then I want to study logic. If I don't want to be a lawyer, then I don't like to argue. Therefore, if I like to argue, then I want to study logic. A. Valid B. Invalid EXAMPLE 2.1.15 I will hire Gomer or I will hire Homer. If I don't hire Homer then I'm not having a bad hair day. I don't hire Gomer. Therefore I'm having a bad hair day. A. Valid B. Invalid EXAMPLE 2.1.16 Test the validity of the following argument: If I buy cheap gasoline, then my car runs badly. If I don't change the oil, then my car runs badly. Therefore, if I buy cheap gasoline, then I don't change the oil. A. Valid B. Invalid
Step 1: Symbolize the argument.
Let p be the statement "One grows vegetables."
Let q be the statement "One is a gardener."
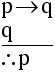
Generalizing from the result of EXAMPLE 2.1.6, we have this fact:
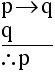
will be an invalid argument.
If I eat Wheaties, then I am healthy.
I am healthy.
Therefore, I eat Wheaties.
Thus, Thoreau was a great writer.
All men are mortal. Socrates is a man. Therefore, Socrates is mortal.
Recall that a universal statement such as "All men are mortal" can be
written equivalently as an "if...then" statement:
"If one is a man, then one is mortal," or, even more generally,
Let p be "(Subject) is a man."
Let q be "(Subject) is mortal."
Then, letting "Socrates" be the subject of these statements,
the argument has this form:
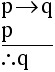
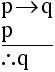
is a valid argument.
I did quit school.
Therefore, I sell apples on the corner.
Steve is a Gator.
Thus, Steve is obnoxious.
Diogenes is a beggar.
Hence, Diogenes is not a chooser.
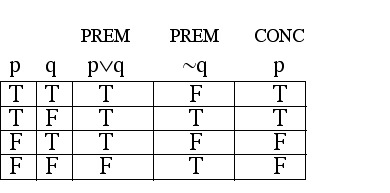
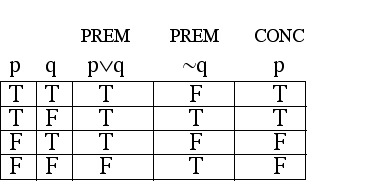
I'm not locked out.
Therefore, I have my keys.
Let q be the statement "I'm locked out." ![]()
![]()
will be a valid argument. ![]()
Socrates is in Athens or Socrates is in Sparta.
Socrates isn't in Sparta.
Thus, Socrates is in Athens.
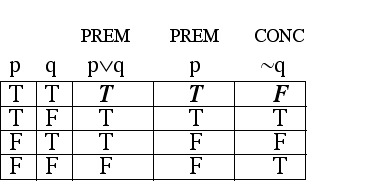
I'm walking.
Therefore, I'm not chewing gum.
Let q be the statement "I chew gum."![]()
![]()
![]()
is automatically INVALID.
The Argue-Mentor
EXAMPLE 2.1.10