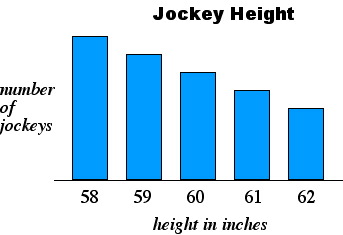
EXAMPLE 2.10.4

The graph below shows the distribution according to height of a group of jockeys at a south Florida horse track. Select the statement that correctly describes a relationship between measures of central tendency for this distribution.

A. The mean is less than the mode.

B. The mode and the mean are the same.

C. The median is greater than the mode.

D. The median and the mean are the same.

SOLUTION

In this distribution we know that the mode is 58, because 58 is the value under the tallest column. But 58 is also the smallest value in this distribution. This indicates that both the mean an median should be greater than 58 (because in any collection of numbers that are not all identical, the average will be greater than the smallest number and less than the largest number).

The following statements would be correct:

The mean is greater than the mode.

The mode is less than the mean.

The median is greater than the mode.

The mode is less than the median.

We see that choice C is correct.

Also, referring to the fact that in a skewed distribution the median tends to fall between the mode and the mean, these two statements would also be reasonable:

The median is less than the mean.

The mean is greater than the median.

One last observation:

In the case where the height of the column over the mode was greater than the combined heights of all of the other columns, the median equal to the mode.