EXAMPLE 2.10.7

Whenever Gomer goes for a stroll, he waves at every person who passes by. He finds that nearly half of the people do not wave back (that is, they wave back with zero fingers). Of the others, most wave back with one finger, while some wave back with five fingers. Select the statement that is true regarding this distribution of fingers.

A. The mean is less than the mode.

B. The median is less than the mean.

C. The median is less than the mode.

D. The mean is the same as the median.

SOLUTION

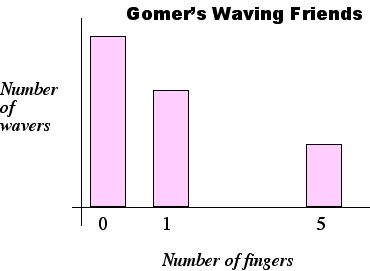
Although we do not know how many respondents are involved, there is enough information for us to make a generally accurate bar graph for this distribution. The bar graph will show three values: 0, 1 and 5. The tallest bar will be over the value 0, since the description indicates that almost as many people waved back with zero fingers as waved back with 1 or 5 fingers. The next tallest column will be over the value 1, and the smallest column will be over the value 5.

This is an example of data skewed to the right.

In data skewed to the right, since the mode is the smallest value in the distribution, the mean and median should both be greater than the mode. The following statements are reasonable:

The mean is greater than the mode.

The median is greater than the mode.

The mode is less than the mean.

The mode is less than the median.

Also, when data is skewed we usually expect that median will fall between the mean and the mode:

The median is less than the mean.

The mean is greater than the median.

We see that choice B is correct.

One last note: in any kind of distribution, if the mode comprises more than half of the data points (that is, if the column over the mode is taller than the heights of all of the other columns combined), then the median would be equal to the mode.