Euler diagrams natural-language arguments
Euler diagrams and arguments involving the word "some."
EXAMPLE 2.3.1
Test the validity of this argument:
All elephants are huge creatures.
Some huge creatures have tusks.
Therefore, some elephants have tusks.
Before we solve this problem, we will point out that this argument is different from any of the arguments that we've encountered so far, in that it involves the word "some."
In our previous work we have relied on the following facts that give the relationships between certain quantified statements and logical connectives.
"All A are B" is equivalent to "If A, then B."
"No A are B" is equivalent to "If A, then not B."
However, the quantifier "some" is not covered by the two rules shown above.
FACT: The statement "Some A are B" is not equivalent to any useful statement involving logical connectives.
Since our construction of truth tables depends upon the properties of logical connectives, the fact above leads to this profound fact about arguments:
FACT: The truth table method is of no practical use when an argument contains at least one statement of the form "Some A are B."
This means that we cannot use a truth table to analyze the argument in EXAMPLE 2.3.1 above. We introduce a different technique for use in cases like this:
ANALYZING ARGUMENTS INVOLVING THE WORD "SOME"
When an argument involves the word "some," we use Venn diagrams to try to show that the argument is INVALID.
An argument is INVALID if we are able to draw a Venn diagram that agrees with every PREMISE but denies the CONCLUSION.
Venn diagrams that are used to analyze arguments are usually called Euler diagrams, in honor of the mathematician Leonhard Euler.
A Venn diagram (Euler diagram) that agrees with every premise but denies the conclusion is called a counterexample to the argument.
Who's to Blame
EXAMPLE 2.3.1 SOLUTION
In order to test the validity of the argument
"All elephants are huge creatures.
Some huge creatures have tusks.
Therefore, some elephants have tusks."
we will try to draw a counterexample. That is, we will try to draw an Venn diagram having circles representing the sets "elephants," "huge creatures," and "creatures having tusks."
The argument will be invalid if and only if it is possible to draw the diagram in such a way that it shows that "all elephants are huge creatures" and also shows that "some huge creatures have tusks" but doesn't show that "some elephants have tusks."
It is also important to remember this basic fact about all arguments:
Whether or not an argument is valid has nothing to do with whether or not the conclusion sounds like a reasonable statement.
We begin with a Venn diagram that agrees with the first premise, "All elephants are huge creatures. This diagram must show the set "elephants" contained within the set "huge creatures."

Next, we expand the diagram to include the second premise, "Some huge creatures have tusks." Thus, we must draw the set of "things with tusks" in such a way that it overlaps the set of huge creatures. In fact there are several ways to do this, including:

Notice that although Figures I and II above both agree with both premises,
Figure I also denies the conclusion (that it, it doesn't agree with "Some elephants have tusks."
Figure I above is a counterexample to the argument; it shows us that the
argument is INVALID.
In fact, the invalid argument in this example is closely related to Fallacy of the Converse.
EXAMPLE 2.3.2
Test the validity of the argument:
All porpoises are intelligent. Some sea mammals are porpoises.
Therefore, some sea mammals are intelligent.
EXAMPLE 2.3.2 SOLUTION
We will try to draw an Euler diagram that is a counterexample to the argument;
that is, we will try to show that the argument is invalid by drawing a
diagram that shows "all porpoises are intelligent" and also shows "some
sea mammals are porpoises" but doesn't show the conclusion "some sea
mammals are intelligent."
We start with a diagram for the first premise, "All porpoises are intelligent." This diagram must show the set of porpoises contained within the set of intelligent things.
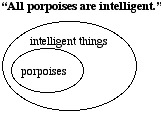
Next, we expand the diagram to include the set of sea mammals in such a way it agrees with the statement "Some sea mammals are porpoises." At the same time, however, we want to try to deny the conclusion "Some sea mammals are intelligent." In this case, we will find that no matter how we try, any diagram that agrees with the two premises with automatically agree with the conclusion.

We have determined that the argument is VALID.
It is important to understand that the argument is valid not because of the particular
diagram shown above, but because in drawing that diagram we realized that a counterexample
is not possible.
In fact, the argument in this example is closely related to Direct Reasoning.
EXAMPLE 2.3.3
Test the validity of the argument:
All cows like to chew. Some dairy animals don't like to chew.
Therefore, some dairy animals aren't cows.
EXAMPLE 2.3.3 SOLUTION
Any diagram that agrees with both premises must show both of these relationships:
The set of cows must be contained within the set of things that like to chew, and; at least some small part of the set of dairy animals must lie outside of the set of things that like to chew. There are many ways to accomplish this, but all of them with automatically show that at least some dairy animals (namely, the ones who don't like to chew) aren't cows:
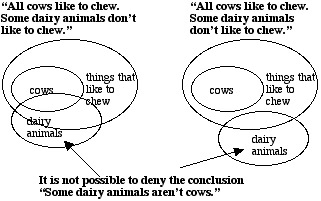
The argument is VALID; it is important that we understand, however,
that the argument is valid not because of either of the particular diagrams shown above,
but because we have cometo the realization that any diagram that
agrees with both premises will automatically agree with the conclusion;
that is, a counterexample is not possible.
The argument in this example is closely related to Contrapositive Reasoning.
EXAMPLE 2.3.4
Test the validity of the argument:
Some lawyers are judges. Some judges are politicians.
Therefore, some lawyers are politicians.
EXAMPLE 2.3.4 SOLUTION
Before we draw any diagrams, we re-emphasize: The validity of an argument has
nothing to do with whether or not the conclusion sounds like a reasonable statement. In fact, this argument is INVALID, as the Euler diagram below shows clearly:
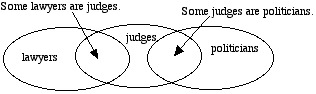
The diagram agrees with both premises but denies the conclusion.
You probably see that we could also draw a diagram that agrees with both premises
and also agrees with the conclusion. It is vital that you understand that such
a diagram does not make the argument valid; what makes an argument valid
is impossibility of drawing a counterexample.
EXAMPLE 2.3.6
Test the validity of each argument.
A. Some fish are tasty. All fish can swim. Therefore, some tasty things can swim.
B. Some doctors are dentists. Some dentists are surgeons. Therefore, some doctors are surgeons.
C. All hogs are smelly. Some swine aren't hogs. Therefore, some swine aren't smelly.
D. All burglars are criminals. Some thieves are criminals. Therefore, some burglars are thieves.
E. Some food preparers aren't cooks. All chefs are cooks. Some food preparers aren't chefs.
F. No thieves are saintly. Some congressmen are thieves. Therefore, some congressmen arenÍt saintly.
EXAMPLE 2.3.6 SOLUTIONS
A. VALID
B. INVALID
C. INVALID
D. INVALID
E. VALID
F. VALID
EXAMPLE 2.3.7
Consider these premises:
All poodles are dogs. All dogs bark.
We should easily recognize that a valid conclusion is "All poodles bark."
Question: since "All poodles bark" is a valid
conclusion, wouldn't "Some poodles bark" also be a valid conclusion?
After all, "some" sounds like a softer condition than "all," so common sense suggests that "some A are B" should be a valid conclusion whenever "all A are B" is a valid conclusion.
However, the answer to the question above is "no." In fact, "all" does not imply "some," due to this peculiarity
of the word "all:" A statement like "All poodles bite" is true, even
if there were no poodles. In other words, if all of the poodles went extinct,
the statement "All poodles bite" would still be (vacuously) true, but
the statement "Some poodles bite" would be false (because "some" means "at least one").
This example gives rise to the following general observation, which holds for all arguments.
If every premise in an argument has the form "All are...," a valid
conclusion will not have the form "Some are..." (...unless a premise
specifies that all of the sets in the argument are non-empty).
Download practice exercises (PDF file)