EXAMPLE 2.5.3

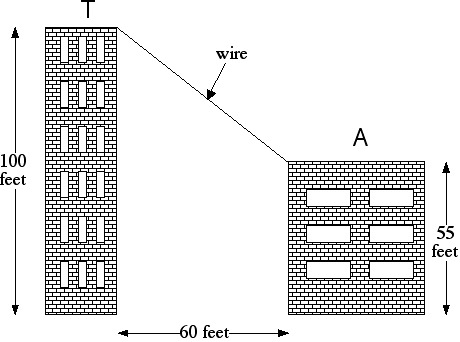
The figure below shows the Math Department's plan to run a computer cable (w) from the top of the Algebra Building (A) to the top of the Trig Tower (T). Find the total cost of the cable, assuming that it costs $3.50 per foot. (The front faces of the buildings, and the cable, are all in the same plane.)

A. $75

B. $21

C. $263

D. $753

SOLUTION

We need to find the length of the wire (in feet) and multiply by the cost factor of $3.50 per foot.

We can find the length of the wire by recognizing that the wire is the hypotenuse of a right triangle whose legs measure 60 feet and 45 feet respectively (the 45-foot height is obtained by subtracting the height of the Algebra Building from the height of the Trig Tower). Let L be the length of the wire. According to the Pythagorean Theorem,

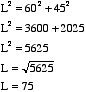
The length of the wire is 75 feet, and the cost is $3.50 per foot, so the total cost is (75)($3.50) = $262.50. The best choice is C.