EXAMPLE 2.9.1
Survey question: How many books did you buy this semester?
Responses: 5, 8, 4, 0,10,4, 6, 7, 4, 2, 10
What was the typical response?
MEASURES of CENTRAL TENDENCY
A measure of central tendency is a number that represents the typical value in a collection of numbers. Three familiar measures of central tendency are the mean, the median, and the mode.
We will let n represent the number of data points in the distribution. Then
(The mean is also known as the "average" or the "arithmetic average.")
Median = "middle" data point (or average of two middle data points) when the data points are arranged in numerical order.
Mode = the value that occurs most often (if there is such a value).
In EXAMPLE 2.9.1 the distribution has 11 data points, so n = 11.
MEAN = (5 + 8 + 4 + 0 + 10 + 4 + 6 + 7 + 4 + 2 + 10)/11
= 60/11 = 5.45 (this has been rounded).
We cansay that the typical respondent bought 5.45 books.
We can also use the MEDIAN to describe the typical response. In order to find the median we must first put the data points in numerical order:
0, 2, 4, 4, 4, 5, 6, 7, 8, 10, 10
Now we choose the number in the middle of the list.
0, 2, 4, 4, 4, 5, 6, 7, 8, 10, 10
The median is 5.
Because the median is 5 it is reasonable to say that the typical respondent bought 5 books. Notice that there were just as many people who purchased 5 books or more as there were people who purchased 5 books or fewer.
We can also use the MODE to describe the typical response to the survey. Since the number 4 occurs more often than any of the other numbers on this list, the mode is 4.
EXAMPLE 2.9.2
Survey question: How many semester hours are you taking this semester?
Responses: 15, 12, 18, 12, 15, 15, 12, 18, 15, 16
What was the typical response?
see solution
FINDING THE "MIDDLE" OF A LIST OF NUMBERS
In the two previous examples, we found the median by first arranging the list numerically and then crossing off data points from each end of the list until we arrived at the middle. This method works well as long as there are relatively few data points to work with. In cases where we are dealing with a large collection of data, however, it is not a practical method for finding the median.
If n represents the number of data points in a distribution, then:
the position of the "middle value" is
If the data points have been arranged numerically, we can use this fact to efficiently find the median.
Example:
For the following list, n = 19.
24, 25, 28, 31, 33, 33, 36, 42, 42, 48, 51, 57, 57, 68, 75, 79, 79, 79, 85
The numbers are already in numerical order. The position of the "middle of the list" is:
(n+1)/2 = (19+1)/2 = 20/2 =10
Thus, the tenth number will be the median:
24, 25, 28, 31, 33, 33, 36, 42, 42, 48, 51, 57, 57, 68, 75, 79, 79, 79, 85
The median is 48.
EXAMPLE 2.9.3
Compute the mean, median, and mode for this distribution of test scores:
92, 68, 80, 68, 84
see solution
EXAMPLE 2.9.4
To paraphrase Benjamin Disraeli: "There are lies, darn lies, and DAM STATISTICS."
Compute the mean, median and mode for the following DAM STATISTICS:
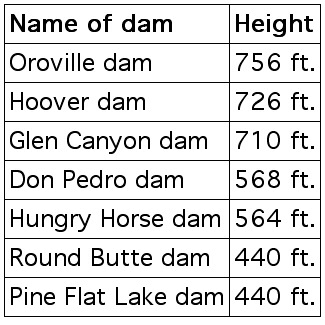
see solution
FREQUENCY TABLES
EXAMPLE 2.9.5
Find the mean, median and mode for the following collection of responses to the question: "How many parking tickets have you received this semester?"
1, 1, 0,1, 2, 2, 0, 0, 0, 3, 3,0, 3, 3, 0,2, 2, 2, 1, 1,4, 1, 1,0,3, 0, 0, 0, 1, 1, 2, 2, 2, 2,1, 1, 1, 1, 4, 4, 4,1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2,1, 1, 1, 1, 13,3,0, 3, 3, 1, 1, 1, 1,0, 0, 1, 1, 1, 1, 3, 3, 3, 2, 3, 3, 1, 1, 1,2, 2, 2,4, 5, 5, 4, 4, 1, 1, 1, 4,1, 1, 1,3, 3, 5,3, 3, 3, 2,3, 3, 0, 0, 0, 0, 3, 3, 3, 3, 3, 3, 0, 2, 2, 2, 2, 1, 1, 1,3, 1, 0, 0, 0,1, 1, 3,1, 1, 1, 2, 2, 2, 4, 2, 2, 2, 1, 1, 1, 1,0, 0, 2, 2, 3, 3,2, 2, 3,2, 0, 0, 1, 1,3, 3, 3, 1, 1, 1, 1, 1,2, 2, 2, 2, 1, 1, 1, 1, 0,1, 1, 1, 3,1, 1, 1, 2, 2, 2, 1, 1, 1,2, 1, 1, 1,3, 3,5, 3, 3, 1, 1, 1, 3, 3, 3, 3, 1, 1, 1,4, 1, 1, 4, 4, 4, 4, 4, 4,1, 1, 1,2, 2,5, 5, 2, 3, 3, 4, 4,3,2, 2, 2, 1,5, 1,2, 2, 1, 1, 1, 2, 2, 2, 2, 2,1, 1, 0,1, 1, 1,3, 3, 3, 3, 3
EXAMPLE 2.9.5 SOLUTION
It will be much easier to work with this unwieldy collection of data if we organize it first. We will arrange the data numerically.
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3,
4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4,
5, 5, 5, 5, 5, 5, 5
The value "0" appears 27 times.
The value "1" appears 96 times.
The value "2" appears 58 times.
The value "3" appears 54 times.
The value "4" appears 18 times.
The value "5" appears 7 times.
We can summarize the information above in the following frequency table:
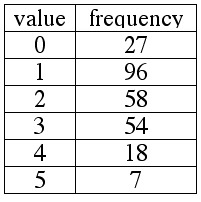
From the previous example we generalize to form this rule for determining
the median for data in a frequency table (this rule assumes that the values
appear in the table in numerical order).
Make a column for cumulative frequency as follows:
1. The cumulative frequency of the first row is the same as the frequency of the first row.
2. For every other row, determine cumulative frequency by adding the frequency of that
row to the cumulative frequency of the previous row.
When cumulative frequency first equals or exceeds 
, stop and use the value in that row for the median. ( If 
is exactly .5 greater than one of the cumulative frequencies, then the median will be the average of the associated values from that row and the next row).
EXAMPLE 2.9.6
The frequency table below represents the distribution of scores on a ten-point quiz.
Compute the mean, median, and mode for this distribution.
Quiz Scores
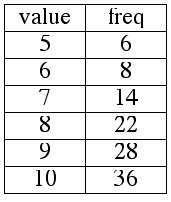
EXAMPLE 2.9.7
The frequency table below represents the distribution, according to age, of students in a certain class.
Ages of Students
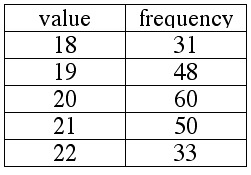
1. Find the mean, median, and mode for this distribution.
2. True or false: 18 students were 31 years old.
EXAMPLE 2.9.8
Compute the mean, median and mode for the data in the frequency table below.
The data represents the distribution of households according to the number of cars per household.
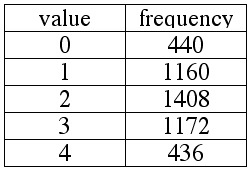
Find the mean, median, and mode.
EXAMPLE 2.9.9
A number of people invested $1000 each in the Gomer Family of Mutual Funds.
The frequency table below shows the current values of those investments.
Compute the mean, median and mode.
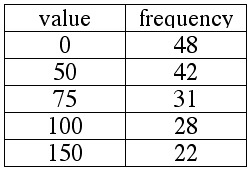
EXAMPLE 2.9.10
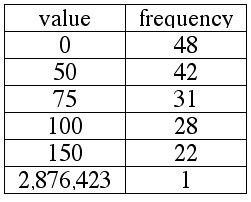
A number of people invested $1000 each in the Gomer Family of Mutual Funds.
The frequency table below shows the current values of those investments after
Gomer hit the trifecta at the dog track, and hit the Cash 5 jackpot.
Compute the mean, median and mode.
EXTREME VALUES and THEIR EFFECTS ON MEAN, MEDIAN and MODE
If we compare the previous two examples, we see that the two distributions are nearly identical,
except that the distribution in EXAMPLE 2.9.10 contains one extra number (2,876,423) that is
significantly greater than any of the other numbers in the distribution.
(A number that is significantly greater or significantly less than most of the other numbers in a
distribution is called an extreme value or outlier.)
Notice that this including this extreme value had a huge effect on the mean of the distribution
(which increased from $61.55 to $16,784.58) but had no effect whatsoever on
either the median or the mode. Also notice that in the distribution in EXAMPLE 2.1.10,
the mean is not a good representation of the typical value in the distribution.
This illustrates an important general fact:
Of the three measures of central tendency (mean, median, mode), the mean is the
measure that is most likely to be distorted by the presence of extreme values.
EXAMPLE 2.9.11
A number of people were asked "How many legs does your favorite animal have?"
The responses are summarized below.
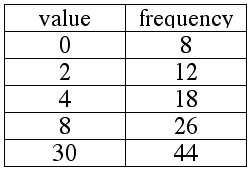
1. Find the mean, median and mode.
2. True or false: There were no people who said that their favorite animal had 8 legs.
EXAMPLE 2.9.12
Members of the preview audience for the new Arnie Schvartzengagger film,
The Predagagger XII: Things Blow Up, were asked to rank the film from 0 ("stinks like a dead cyborg") to 6 ("XII thumbs up!"). The results are summarized in the table below.
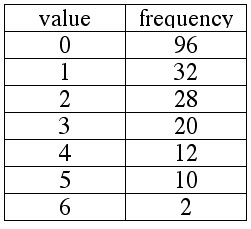
1. True or false: The median is 3.
2. True or false: The mean is 3.
3. True or false: Twenty-eight people gave the film a rank of 2.
4. True or false: 128 people gave the film a rank of less than 28.
EXAMPLE 2.9.13
The annual earnings for employees of a certain restaurant are given below:
12 laborers earn $8000 each.
10 laborers earn $9000 each.
4 supervisors earn $11000 each
The owner/manager earns $240,000.
Of the three measures of central tendency, which will be the least accurate representation of
"typical earnings?"
EXAMPLE 2.9.14
The table below shows the distribution of scores for Quiz #3 in MGF1106
sections 01 - 08, Spring '99.
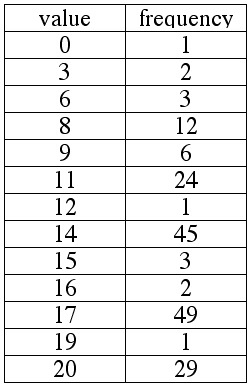
1. Find the mean.
A. 11.54
B. 14.54
C. 13.69
D. 17
2. Find the median
A. 17
B. 12
C. 13
D. 14