PROBABILITIES INVOLVING "OR," "NOT"
Probabilities involving "or", "not"
In general:
P(E or F) = P(E) + P(F) - P(E and F)
P(not E) = 1 - P(E)
(Note: these problems can frequently be analyzed with Venn diagrams as well.)
EXAMPLE 3.5.1
According to a recent article from the New England Journal of Medical Stuff ,
63% of cowboys suffer from saddle sores,
52% of cowboys suffer from bowed legs,
and 40% suffer from both saddle sores and bowed legs.
What is the probability that a randomly selected cowboy...
1. ...has saddle sores or bowed legs?
2. ...doesn't have saddle sores?
3. ...has saddle sores but doesn't have bowed legs?
4. ...has saddle sores and bowed legs?
5. ...has neither of these afflictions?
EXAMPLE 3.5.2
A survey of 50 Yugo drivers revealed the following:
30 enjoy waiting for tow trucks
35 enjoy hitchhiking
25 enjoy waiting for tow trucks and hitchhiking
What is the probability that a randomly selected Yugo driver...
1. ...enjoys at least one of these activities?
A. .8
B. .65
C. .9
D. 1.8
2. ...doesn't enjoy hitchhiking?
A. .35
B. .15
C. .3
D. .5
3. ...enjoys neither of these activities?
EXAMPLE 3.5.3
The table below shows the distribution of guests on the Jerry Slinger show.
S: screams obscenities
P: punches somebody
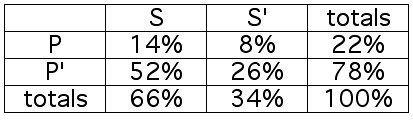
1. What is the probability that a guest screams
obscenities or punches somebody?
2. What is the probability that a guest doesn't scream obscenities and
doesn't punch anybody?
MUTUALLY EXCLUSIVE EVENTS
Events E and F are mutually exclusive if it is not possible for
both E and F to occur simultaneously.
This means that P(E and F) = 0.
If events E, F are mutually exclusive, then P(E or F) = P(E) + P(F)
EXAMPLE 3.5.4
In a certain class, 45% of the students are freshmen (F),
30% are sophomores (So)
20% are juniors (J),
5% are seniors (Se)
What is the probability that a randomly chosen student is a junior or senior?
EXAMPLE 3.5.5
A university awards scholarships on the basis of student
performance on a certain placement test. The table below
indicates the distribution of scores on that test.
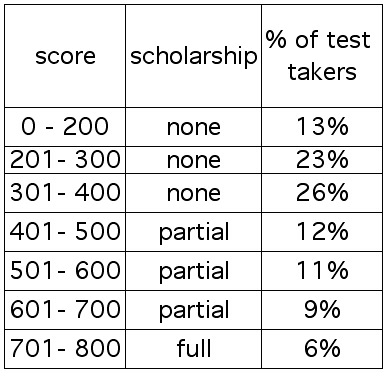
If one student is randomly selected, find the probability that he/she...
1. ...received a partial scholarship.
2. ...didn't have a score in the 201 - 300 range.
3. ...had a score less than 501
4. ...received some kind of scholarship
If 800 students are selected, how many would we expect...
5. ...received no scholarship?
6. ...had scores higher than 600?
EXAMPLE 3.5.6
The pie chart below shows the distribution of animals at Gomer's Petting Zoo.
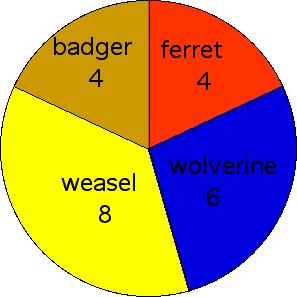
If one animal randomly goes on a rampage, find the probability that it is...
1. ...a weasel or badger?
2. ...not a badger or ferret?
UNIT 3 MODULE 6
INDEPENDENT EVENTS, THE MULTIPLICATION RULES, CONDITIONAL PROBABILITY
EXAMPLE 3.6.1
Suppose we have one six-sided die, and a spinner such as is used in a child's game.
When we spin the spinner, there are four equally likely outcomes: "A," "B," "C," and "D."
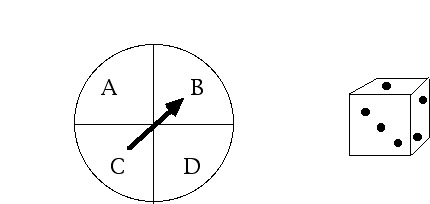
An experiment consists of rolling the die and then spinning the spinner.
How many different outcomes are possible?
What is the probability that the outcome will be "3-C?"
The MULTIPLICATION RULE for INDEPENDENT EVENTS
If E and F are independent events, then
![]()
Recall this (authentic) data from the Natural Resources Defense Council:
40% of bottled water samples are merely tap water.
30% of bottled water samples are contaminated by such pollutants as arsenic and fecal bacteria.
If two samples are independently selected, what is the probability that both samples are
contaminated by pollutants?
EXAMPLE 3.6.6
Suppose that survey of hawks reveals that 40% of them agree with the
statement "Poodles are tasty." If two hawks are independently selected, what is the probability that neither of them agree that "Poodles are tasty?"
A. .8
B. .6
C. .36
D. .64
INDEPENDENT EVENTS, DEPENDENT EVENTS
Two events A and B are said to be independent if they do not influence one
another. More formally, this means that the occurrence of one event has no effect upon
the probability of the other event.
EXAMPLE 3.6.2
1. Let E be the event: "A randomly chosen person drives a white car."
Let F be the event: "A randomly chosen person has a sister who lives in Alabama."
These events are independent, because there is no apparent reason why a the place of
residence of a person's sister would have any influence on a person's car-buying habits.
These two conditions do not apparently influence one another.
2. Let E be the event: "Today is your birthday."
Let F be the event: "The fourth digit in your SSN is '7'"
These events are independent, since there is no apparent reason why a certain digit in your
SSN should have any connection to whether or not today is your birthday.
These two conditions do not influence one another.
3. Let E be the event: "You are wearing a cast on your left arm."
Let F be the event" "Your left arm is broken."
These two events are not independent, because a person wearing a cast is more
likely to have a broken limb than is a person who isn't wearing a cast.
The occurrence of one of these events affects the probability of the other event.
Such events are said to be dependent.
4. Let E be the event: "A randomly chosen voter is a registered Democrat."
Let F be the event: "A randomly chosen voter voted for Bill Clinton."
These events are not independent, because a registered Democrat is more likely to have voted
for Bill Clinton than is a person who isn't a registered Democrat.
The occurrence of one of these events increases the probability of the other event.
Such events are said to be dependent.
5. Let E be the event: "A person is left-handed."
Let F be the event: "A person is right-handed."
Are these events independent?
6. Let E be the event "A person is right-handed."
Let F be the event "A person is named Joe."
Are these events independent?
EXAMPLE 3.6.3
At the entrance to a casino, there are two slot machines.
Machine A is programmed so that in the long run it will produce a winner in 10% of the plays.
Machine B is programmed so that in the long run it will produce a winner in 15% of the plays.
1. If we play each machine once, what is the probability that we will win on both plays?
2. If we play each machine once, what is the probability that we will lose on both plays?
3. If we play each machine once, what is the probability that we will win on at least one play?
EXAMPLE 3.6.5
According to a study in 1992 by the U.S. Department of Agriculture, 80% of commercially grown
celery samples and 45% of commercially grown lettuce samples contain traces of agricultural
poisons (insecticides, herbicides, fungicides).
If Homer eats one serving (one sample) of celery and one serving of lettuce:
1. What is the probability that both the celery and the lettuce contain traces of agricultural poisons?
2. What is the probability that neither serving contains traces of agricultural poisons?
3. What is the probability that at least one of the servings contains traces of agricultural poisons?
EXAMPLE 3.6.7
Real data (as of 1999):
Each day, 7% of the US population eat a meal at McDonald's.
If two people are randomly and independently selected, what is the probability that...
1. ...both people will eat a meal at McDonald's today?
2. ...neither person will eat a meal at McDonald's today?
3. ...at least one of them will eat a meal at McDonald's today?
EXAMPLE 3.6.8
The table below shows the results of a survey of TV viewing habits:
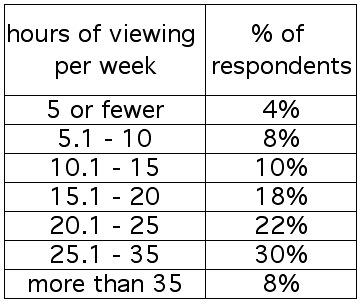
Assume that Homer and Gomer are a couple of randomly selected, independent guys.
According to the data in the table above, what is the probability that:
1. Homer views TV for 5 or fewer hours per week, and Gomer views TV for 10.1 - 20 hours per week?
2. Homer views TV for 35 or fewer hours per week, and so does Gomer?
Still assuming that Homer and Gomer are a couple of randomly selected, independent guys:
3. What is the probability that neither of them falls in the 15.1 - 20 hours per week category?
4. What is the probability that at least one of them views TV for 15.1 - 20 hours per week?
EXAMPLE 3.6.9
A university awards scholarships on the basis of student performance on a certain placement test.
The table below indicates the distribution of scores on that test.
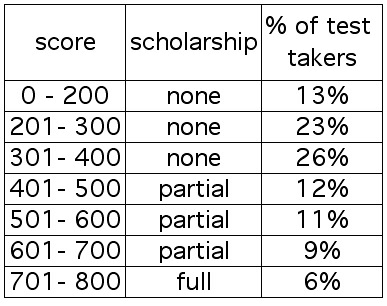
If Homer and Gomer are a couple of randomly selected, independent guys, what is
the probability that neither of them received a scholarship?
CONDITIONAL PROBABILITY
On the Impossibility of Tuesday
A dialogue
Homer: It's Tuesday.
Gomer: Are you sure?
Homer: Sure I'm sure.
Gomer: Really? But it can't be Tuesday, can it?
Homer: Of course it's Tuesday. Yesterday was Monday, today is Tuesday.
Gomer: But that's exactly the problem.
Homer: What problem?
Gomer: The problem of Tuesday. It can't be Tuesday.
Homer: Whatever.
Gomer: Look, there are seven days in a week, right?
Homer: Last time I checked.
Gomer: So if I just woke up from a coma--
Homer: --that would be a nice change--
Gomer: --if I just woke up from a coma, and didn't know what day it was, the probablity that today
is Tuesday would be one seventh, right?
Homer: Right; one out of seven.
Gomer: But in order for today to be Tuesday, yesterday must have been Monday.
Homer: It follows.
Gomer: Actually, it precedes. But the probability that yesterday was Monday is also one seventh,
so the probability that yesterday was Monday AND today is Tuesday is only one seventh of one seventh...
Homer: ...The multiplication rule.
Gomer: Right, so that's only one out of 49. And it gets worse. In order for yesterday to have been Monday, the day before
yesterday would have had to have been Sunday...
Homer: ...so the probability that the day before yesterday was Sunday, AND yesterday was Monday,
AND today is Tuesday...
Gomer: ...is one seventh of one seventh of one seventh...
Homer: ...which is only, let's see, (mumbles, makes calculations in the air with finger, carries the six, et c)
one out of 343, I guess. Dang. Maybe today isn't Tuesday, after all.
Gomer: Now, I'm especially worried, because it occured to me that in order for the day before yesterday
to have been Sunday, the day before that would have had to have been Saturday, so (let's work backward here) the probability
that today is Tuesday AND yesterday was Monday AND the day before yesterday was Sunday AND the
day before that was Saturday...
Homer: ...is one seventh of one seventh of one seventh of one seventh, which is ...
Gomer: ...one out of 2401.
Homer: Hey, you're pretty quick with that.
Gomer: Well, I've been researching the matter. In fact, I found out that if you take this
back as far as a week and a half, it's obvious that the probability that today is Tuesday is
only about one in 282 million.
Homer: A virtual impossibility!
Gomer: So, I wonder what day it is.
Homer: Me too, now that you've explained the situation to me.
Gomer: One thing's for sure.
Homer: You've got that right. One thing's for sure: today isn't Tuesday.
Gomer: Exactly.
Homer: It's a virtual impossibility.
Gomer: There is a bright siide, though.
Homer: And that is?
Gomer: Well, I was supposed to have a math test on Tuesday, but I haven't been studying.
Homer: Clearly, you've had more important fish to fry.
Gomer: Well put; I've been wrestling with this "impossibility of Tuesday" issue for quite a while.
At least one thing is virtually certain: my math test can't be today.
Homer: It's virtually impossible.
Gomer: That's a relief.
Homer: Every cloud has its silver lining. I have get going, though. I have term paper due tomorrow.
Gomer: Wednesday?
Homer: Yeah. Wednesday morning, eight o'clock sharp.
Gomer: But it's virtually impossible that tomorrow will be Wednesday...
Suppose we roll one die.
Let A be the event that the result is the number "2."
Then we know that
![]()
However, suppose that before I reveal the result of the die roll, I tell you that an
even number has occurred (event E).
Would you still say that
![]()
This is an example of CONDITIONAL probability.
We say that
"The probability that the die roll is '2,' given that the die roll is 'even,' is 1/3.
Notation:
![]()
or
![]()
General fact:
For any events E, F
![]()
which is the same as
![]()
If we are referring to population statistics,
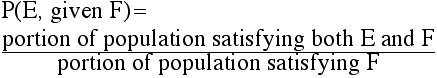
EXAMPLE 3.6.10
In a box we have a bunch of puppies:
4 brown bulldogs
2 gray bulldogs
5 brown poodles
3 gray poodles
If one puppy is selected, what is the probability that the puppy is...
1. ...brown?
2. ...a poodle?
3. ...gray or a bulldog?
4. ...brown and a bulldog?
5. ...a bulldog, given that it is gray?
6. ...brown, given that it is a poodle?
EXAMPLE 3.6.11
A survey of Gators indicates that 7% are charming, 4% are modest, and 3% are
both charming and modest. Find the probability that a Gator is modest, given
that he/she is charming.
A. .75
B. .03
C. .43
D. .25
EXAMPLE 3.6.12
Refer to the data on scholarships in the table presented earlier (see EXAMPLE 3.6.9).
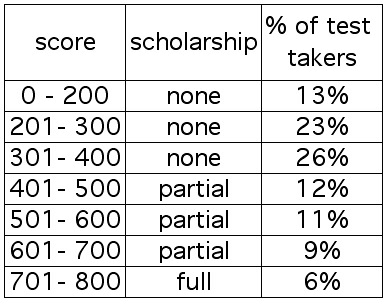
2. What is the probability that a randomly chosen student received a scholarship,
given that he/she had a score less than 501?
EXAMPLE 3.6.13
The table below shows the distribution according to cumulative GPA of
juniors at Normal University.
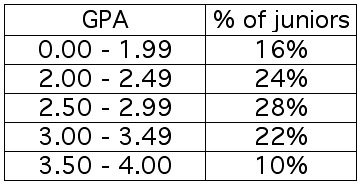
1. Find the probability that a randomly selected junior's GPA is greater than 1.99,
given that it is less than 3.50.
A. .22
B. .88
C. .82
D. .74
2. Referring to the data above, find the probability that a randomly selected
junior's GPA is in the 2.50 - 3.49 range, given that it is greater than 1.99.
EXAMPLE 3.6.14
Recently, Gomer took his Yugo to Honest Al's Yugo Repair Shop for a brake job.
Later, while driving home, a wheel fell off of the car.
When Gomer returned to Honest Al's to complain that the wheel must have fallen off
because of the brake job was done incorrectly, Honest Al produced a ream of statistics
from NHTSA that showed that for this type of brake job, the probabilty that the wheel
will fall off, even if the work is done incorrectly, is only about 0.008.
Based on that data, Honest Al graciously offered to cover 1% of the cost of repairing
the damage to Gomer's car.
What question should Gomer have asked?
C: work done correctly F: wheel fell off
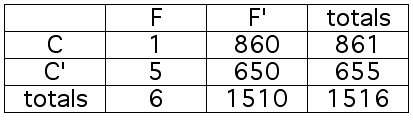
EXAMPLE 3.6.15
Suppose that the data below comes from the FBI Uniform Crime Statistics.
It conveys information about the number of Americans (per 100,000 population)
involved in the crimes of toad theft and toad smoking.
Per 100,000 population: 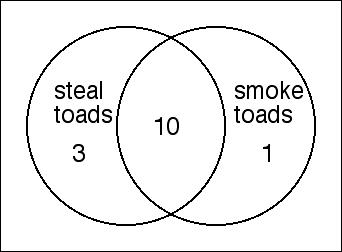
A rare, exotic toad has been stolen from the Tallahassee Museum.
Police are searching for Gomer, who is the only known toad-smoker in town.
Meanwhile, Gomer's lawyers have spoken out publicly. Referring to the data shown above,
they state that, since only 10 out 100,000 people are both toad-stealers and a toad-smokers,
it is extremely unlikely that Gomer is the guilty party, and so the police
should focus their investigation elsewhere.
What do you think about this claim?
EXAMPLE 3.6.16
This situation actually occurred in Southern California a few years ago:
a woman (we'll refer to her as "Nicole") was brutually murdered.
The prime suspect was her ex-husband, a celebrity who had a record of domestic
violence during their short-lived marriage. The ex-husband's defenders issued the
following statistically reasonable statement: "Even if a woman has been the
victim of domestic abuse at the hands of her husband, the probability that she will
be murdered by her husband is only 1 in 1000. Therefore, it is extremely unlikely
that [Mr. ex-Husband] committed the murder."
What, if anything, is wrong with this use of statistics?
EXAMPLE 3.6.17
The conventional test for tuberuculosis (TB) is only about 50% accurate.
Does this mean that if you test positive for TB, then the probability that you
actually have TB is about .5? Suppose that the table below summarizes the results
of the TB screening for a sample of 500 people.
In this table, TB means "A person has tuberculosis," and P means "A person tests
positive for TB."
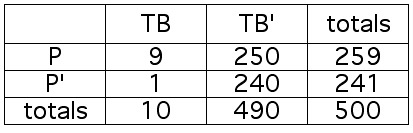
Use this information to find the probability that a person who tests positive for
TB actually has the disease.
EXAMPLE 3.6.18
An IRS auditor has a list of 12 taxpayers whose tax returns are questionable.
The inspector will choose 2 of these people to be audited. Eight of the taxpayers
are Floridians and 4 are Georgians. What is the probability that both people selected
will be Floridians?
THE MULTIPLICATION RULE FOR DEPENDENT EVENTS.
If E and F are dependent, then
![]()
This rule is especially useful when we have a two-step experiment where the outcome of the
first step affects the possible outcomes for the second step, such as the previous example.
EXAMPLE 3.6.19
In his pocket, Gomer has 3 red, 5 orange and 2 blue M&Ms.
If he randomly chooses two M&Ms, what is the probability that both will be red?
A. .6
B. .09
C. .067
D. .52
EXAMPLE 3.6.20
The Skuzuzi Kamikaze sport/utility vehicle is manufactured at two plants,
one in Japan and one in the US. Sixty percent of the vehicles are made in the US,
while the others are made in Japan. Of those made in the US, 5% will be recalled
due to a manufacturing defect. Of those made in Japan, 3% will be recalled.
Find the probability that a vehicle will be...
1. ...made in the US and not recalled.
2. ...made in Japan and recalled.
EXAMPLE 3.6.21
The state insurance commission revealed the following information about the
Preferential Insurance Company's homeowners' insurance: 10% of the policy-holders
have filed more than 5 claims over the past two years; 60% of these people have had
their insurance canceled; 90% of the policy-holders have filed 5 or fewer claims over
the past two years; 15% of these people have had their insurance canceled.
What is the probability that a policy holder filed more than 5 claims over the past
2 years and had his/her insurance canceled?
EXAMPLE 3.6.22
A local sports talk radio station offers the following contest: each Thursday during the
football season, listeners are invited to call the station and make
four predictions "against the spread." The caller may choose any four
college or professional games he/she desires, as long as they are games for which the
odds makers have issued a betting line.
Any caller who turns out to be correct on all four predictions will win a $10 bar tab
from a local sports bar. If we assume that each week 25 callers will get on the air
with their predictions, what will be the expected weekly cost in bar tabs to the bar
that sponsors the program? (In order to answer this question, we need to make a reasonable
assumption about the significance of "beating the point spread.")
EXAMPLE 3.6.23
The world famous Car and Goats problem
You are a contestant on the extinct TV game show Let's Make a Deal.
On the stage, there are three large doors. Behind one door is a new car;
behind the other two doors are goats. You are asked to pick one of the doors.
You win whatever prize is behind the door that you pick.
You choose a door. Before he reveals your prize, the host opens one of the
doors that you didn't pick, and shows you that there was a goat behind that door.
There are still two unopened doors. You have chosen one of them. You now know for
sure that behind one of the two doors is a car, and behind the other door is a goat.
The host asks you if you want to change your choice of doors.
Is there any mathematical reason why you should switch?
To decide whether or not it is advantegeous to switch, answer the following questions:
What is the probability that you will win a car by switching?
What is the probability that you won't win a car by switching?
These two questions are easy to answer, if you think carefully about the underlying conditions:
How could you win (a car) by switching?
How could you lose by switching?
EXAMPLE 3.6.24
The "Year-ending-in-zero" presidential curse
It is a well-known fact from American history that presidents who are elected in years
ending with "0," such as 1840, 1960, 1900, and so forth,
tend to have fatally bad luck.
Of those presidents elected in years ending with "0,"
7 have died in office
5 have been shot
4 have been shot and died in office
2 have neither been shot nor died in office
Find the probability that a president elected in a year ending with zero...
1. ...died in office or was shot.
2. ...was shot but didn't die in office.
3. ...was shot, given that he died in office.
4. ...didn't die in office, given that he was shot.
EXAMPLE 3.5.1 SOLUTIONS
As with counting problems, when a probability problem refers to two overlapping categories,
we can organize the information with a Venn diagram.
Since the data was given in terms of percentages, we pretend that the total population is 100.
Then, each of the percentages is just a raw number.
1. The number of cowboys who have saddle sores or bowed legs = 23 + 40 + 12 = 75.
So, P(saddle sores or bowed legs) = 75/100 = .75
2. From the diagram, the number of cowboys who don't have saddle sores is
12 + 25 = 37, so
P(doesn't have saddle sores) = 37/100 = .37
We could also get this answer from the complements rule. Since 63% of the cowboys have
saddle sores, P(has saddle sores) = .63.
Then, P(don't have saddle sores) = 1 - .63 = .37.
3. The diagram shows us that there are 23 cowboys out of 100 who have saddle sores
but don't have bowed legs, so P(has saddle sores but not bowed legs) = 23/100 = .23
4. The diagram shows that 40 cowboys out of 100 have both conditions (this information
was also stated directly at the beginning of the problem), so
P(has saddle sores but not bowed legs) = 40/100 = .40
5. The diagram shows that there are 25 cowboys out of 100 who have neither affliction, so
P(has neither affliction) = 25/100 = .25
EXAMPLE 3.5.3 SOLUTION
Since the data is given in terms of percentages, we will pretend that the total
population of guests is 100.
1. If we identify those cells of the table corresponding to guests who either
scream or punch or do both, we see that there are three such cells. The corresponding numbers are:
14 + 52 + 8 = 74. The probability is 74/100 = .74
We could also get the answer by using the formula P(A or B) = P(A) + P(B) - P(A and B).
P(screams or punches) = P(screams) + P(punches) - P(does both)
= .66 + .22 - .14 = .74
2. The condition "doesn't scream and doesn't punch" is the complement
of the condition from the previous problem, so we can use the answer from the previous problem to get this answer.
P(doesn't scream and doesn't punch) = 1 - P(screams or punches) = 1 - .74 = .26
We could also get this answer from the table: There is one cell in the table corresponding to the condition "doesn't scream and doesn't punch." The number in that cell is 26%, or .26.
EXAMPLE 3.5.4 SOLUTION
A student cannot simultaneously be both a junior and senior, so these conditions are
mutually exclusive.
P(J or S) = P(J) + P(S) = .20 + .05 = .25
If 60 students are selected, how many would we expect to be freshmen or sophomores?
UNIT 3 MODULE 5 HOMEWORK
See SUPPLEMENTARY EXERCISE SET H, G5.8, G5.9
Answers
3.5.2 1. A (40/50 = .8) 2. C (15/50 = .3) 3. 10/50 = .2
3.5.5 1. .12 + .11 + .09 = .32 2. 1 - .23 = .77
3. .13 + .23 + .26 + .12 = .74 4. .12 + .11 + .09 + .06 = .38
5. (.62)(800) = 496 6. (.15)(800) = 120
3.5.6 1. 12/22 = .545 2. 14/22 = .636
EXAMPLE 3.6.2 SOLUTIONS
5. Dependent 6. Independent
EXAMPLE 3.6.3 SOLUTIONS
1. P(Win on Machine A and on Machine B)
= P(Win on Machine A)XP(Win on Machine B) = (.10)(.15) = .015
2. P(lose on Machine A and on Machine B)
+ = P(Lose on Machine A)XP(Lose on Machine B) = (.9)(.85) = .765
3. "Win on at least one" is the complement of "lose on both," so
P(win on at least one) = 1 - P(lose on both) = 1 - .765 = .235
EXAMPLE 3.6.10 SOLUTION
1. P(brown) = 9/14 2. P(poodle) = 8/14
5. P(bulldog, given that it is gray) = 2/5 because there are 5 gray dogs, and 2 of them are poodles
6. P(brown, given that it is a poodle) = 5/8 because there are 8 poodles and 5 of them are brown.
Since the data refers to two overlapping categories, we can organize it with a Venn diagram.
Since the data is expressed as percentages, we will pretend that the total population of Gators is 100.
The diagram shows that there are 4 charming Gators. Among those 4, 3 are modest.
Therefore, P(modest, given charming) = 3/4 = .75.
EXAMPLE 3.6.20 SOLUTION
1. P(Made in US and not recalled) = P(made in US)XP(not recalled, given made in US)
= (.6)(.95) = .57
2. P(made in Japan and recalled) = P(made in Japan)XP(recalled, given made in Japan)
= (.4)(.03) = .012