PROBABILITIES INVOLVING "OR," "NOT"
Probabilities involving "or", "not"
In general:
P(E or F) = P(E) + P(F) minus P(E and F)
P(not E) = 1 minus P(E)
(Note: these problems can frequently be analyzed with Venn diagrams as well.)
EXAMPLE 3.5.1
According to a recent article from the New England Journal of Medical Stuff ,
63% of cowboys suffer from saddle sores,
52% of cowboys suffer from bowed legs,
and 40% suffer from both saddle sores and bowed legs.
What is the probability that a randomly selected cowboy...
1. ...has saddle sores or bowed legs?
2. ...doesn't have saddle sores?
3. ...has saddle sores but doesn't have bowed legs?
4. ...has saddle sores and bowed legs?
5. ...has neither of these afflictions?
SOLUTIONS
1. We apply the general formula P(E or F) = P(E) + P(F) minus P(E and F)
P(saddle sores or bowed legs) = P(saddle sores) + P(bowed legs) minus P(both conditions)
= .63 + .52 minus .4
= .75
2. P(doesn't have saddle sores = 1 minus P(has saddle sores)
= 1 minus .63
= .37
3. Note that since 63% have saddle sores, and 40% have both saddle sores and bowed legs, then
63% minus 40% = 23% have saddle sores but not bowed legs.
So,
P(saddle sores but not bowed legs) = .23
4. Since 40% have both conditions,
P(saddle sores and bowed legs) = .4
5. In answering question #1 above, we found that 75% of the cowboys have at least one of the two conditions. This means that the other 25% have neither condition, so P(neither condition) =.25
EXAMPLE 3.5.2
A survey of 50 Yugo drivers revealed the following:
30 enjoy waiting for tow trucks
35 enjoy hitchhiking
25 enjoy waiting for tow trucks and hitchhiking
What is the probability that a randomly selected Yugo driver...
1. ...enjoys at least one of these activities?
A. .8
B. .65
C. .9
D. 1.8
2. ...doesn't enjoy hitchhiking?
A. .35
B. .15
C. .3
D. .5
3. ...enjoys neither of these activities?
SOLUTIONS
Note that this problem is similar to the previous problem, except that in this case the data isn't given in percentage form. Note that the total population is 50.
1. P(enjoys waiting or enjoys hitchhiking) = P(enjoys waiting) + P(enjoys hitchhiking) minus P(enjoys both things)
= (30 over 50) + (35 over 50) minus (25 over 50)
= (30 + 35 minus 25) over 50
= 40 over 50
= .8
2. P(doesn't enjoy hitchhiking) = 1 minus P(enjoys hitchhiking)
= 1 minus (35 over 50)
= 15 over 50
=.3
3. P(doesn't enjoy waiting and doesn't enjoy hitchhiking)
= 1 minus P(enjoys waiting or enjoys hitchhiking)
= 1 minus .8
= .2
(Note that we used the answer to question #1 to get the answer to question #3.
EXAMPLE 3.5.3
The table below shows the distribution of guests on the Jerry Slinger show.
S: screams obscenities P: punches somebody
| screams | doesn't scream | totals | |
| punches | 14% | 8% | 22% |
| doesn't punch | 52% | 26% | 78% |
| totals | 66% | 34% | 100% |
In case the presentation in the table isn't clear, the table breaks down the population into four mutually exclusive categories:
i. 14% punch and scream
ii. 8% punch but don't scream
iii. 52% don't punch but do sream
iv. 26% don't punch and don't scream
Note that, among other things, a total of 22% punch and a total of 66% scream
1. What is the probability that a guest screams obscenities or punches somebody?
Answer: P(punches or screams) = P(punches) + P(screams) minus P(punches ands screams)
= .66 + .22 minus .14
= .74
2. What is the probability that a guest doesn't scream obscenities and doesn't punch anybody?
ANSWER: Since 26% don't punch and don't scream, this probability is .26
MUTUALLY EXCLUSIVE EVENTS
Events E and F are mutually exclusive if it is not possible for both E and F to occur simultaneously.
This means that P(E and F) = 0.
If events E, F are mutually exclusive, then P(E or F) = P(E) + P(F)
EXAMPLE 3.5.4
In a certain class, 45% of the students are freshmen (F), 30% are sophomores (So)
20% are juniors (J), 5% are seniors (Se)
What is the probability that a randomly chosen student is a junior or senior?
Answer: These events are mutually exclusive.
P(junior or senior) = P(junior) + P(senior)
=.20 + .05
= .25
EXAMPLE 3.5.5
A university awards scholarships on the basis of student performance on a certain placement test. The table below indicates the distribution of scores on that test.
| score | scholarship | percent of test takers |
| score of 0 to 200 | no scholarship | 13% of students |
| score of 201 to 300 | no scholarship | 23% of students |
| score of 301 to 400 | no scholarship | 26% of students |
| score of 401 to 500 | partial scholarship | 12% of students |
| score of 501 to 600 | partial scholarship | 11% of students |
| score of 601 to 700 | partial scholarship | 9% of students |
| score of 701 to 800 | full scholarship | 6% of students |
If one student is randomly selected, find the probability that he/she...
1. ...received a partial scholarship.
Answer: Just add percentages. 12% + 11% + 9 % = 32%
Since 32% received a partial scholarship, the probability is .32
2. ...didn't have a score in the 201 - 300 range.
Answer. Subtract percentages.
Since 23% of students fell into that range, 77% didn't fall into the range, so the probability is .77
3. ...had a score less than 501
Answer. Add percentages.
13% + 23% + 26% + 12% = 74%, so the probability is .74
4. ...received some kind of scholarship
Answer. Add percentages.
12% + 11% + 9% + 6% = 38%, so the probability is .38
If 800 students are selected, how many would we expect...
5. ...received no scholarship?
Answer. First add percentages.
13% + 23% +26% = 62%.
62% of students received no scholarship.
Now, find 62% of 800.
.62 times 800 = 496.
6. ...had scores higher than 600?
Answer. First add percentages.
9% + 6% = 15%
15% of students had scores higher than 600.
Now, find 15% of 800.
.15 times 800 = 120.
EXAMPLE 3.5.6
The pie chart below shows the distribution of animals at Gomer's Petting Zoo.
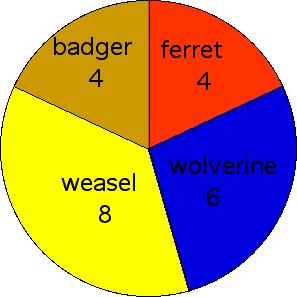
If one animal randomly goes on a rampage, find the probability that it is...
1. ...a weasel or badger?
2. ...not a badger and not a ferret?
ANSWERS
First, find the total number of animals.
4 badgers + 4 ferrets + 8 weasels + 6 wolverines = 22 animals.
1. Since there are 22 animals, and 12 of them are either weasels or badgers, the probability that the random animal is a weasel or badger is 12 divided by 22, or .545.
2. Since there are 22 animals, and 14 of them are not badgers and not ferrets, the probability that the random animal is not a badger and not a ferret is 14 divided by 22, or .636.
Download practice exercises (PDF file)