Suppose that a numerical value (called a payout or a loss) is assigned to each of the outcomes of a random experiment. We define the EXPECTED VALUE as the sum by all products formed by multiplying a payout (or loss) by its probability.
EXAMPLE
Suppose a gambling contest works as follows: one die is rolled. If the result of the die roll is "1" or "2" the player wins $1; if the die roll is "3" or "4" the player wins $3; if the die roll is "5" the player wins $10; if the die roll is "6" the player loses $25. Find the expected value.
SOLUTION
We will summarize the contest with the following Payout Table
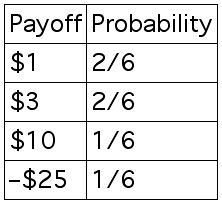
To find the EXPECTED VALUE we find the sum of all terms
formed by multiplying a payout times its probability.
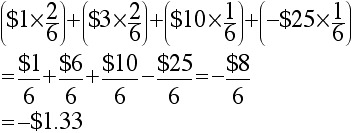
This value represents the long-term average payout.
In other words, if a person played the game many, many times, in the long run
the person would average a loss of $1.33 per play. For instance, if a person
played the game 1000 times, he or she would expect to lose roughly $1,330.
Notice that the process of computing expected value is similar to the process of computing the mean
when data is presented in a frequency table. This corresponds to the fact that the expected value
represents the average payout or loss over the long run.
EXAMPLE
A carnival game works as follows: On a table there are a number of drinking glasses;
each glass contains a live goldfish. The contestant attempts to toss a dime so that it
lands in any one of the glasses. If successful, the contestant wins the goldfish contained therein.
In unsuccessful, the contestant loses the dime. The goldfish is worth 5¢. The game
operator assumes that a contestant will succeed once in every five tries.
From the perspective of the person operating the game, find the expected value of this contest.
ANSWER
If the contestant doesn't win a fish, the game operator experiences a "payout" of 10 cents; the probability that
this will occur is 4/5.
If the contestant wins a fish, the game operator only experiences a "payout" of 5 cents (since the operator
keeps the contestant's dime but forfeits a 5-cent fish); the probability of this payout is 1/5.
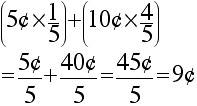
On average the game operator can expect to gain a 9¢ profit each time the game is played.
If the game is played 1,000 times, the operator can expect a proft of $90.
EXAMPLE
A professional bowler is going to purchase a $500,000 insurance policy on his thumb,
in case his career should be cut short by a debilitating thumb injury.
The Gomermatic Corporation specializes in such policies. Their actuaries
estimate that in general, the probability that a bowler will suffer a debilitating
thumb injury is .0002. The company will charge $10,000 for the insurance policy.
From the perspective of the Gomermatic Corporation, what is the expected value of such a policy?
ANSWER
If the bowler doesn't suffer a debilitating thumb injury, the corporation gains $10,000.
The probability of this gain is .9999. If the bowler does suffer such an injury,
the company loses $490,000 (they keep the $10,000 that was initially paid).
The probability of this loss is .0002. The expected value is:
.9998($10,000) + (.0002)(-$490,000) = $9,900
If the company issues a large number of these policies, they
can expect to earn an average of $9,900 per policy.