Set Mathematics
Sets, Elements, Subsets
Any collection of objects can be considered to be a set.
We can define particular sets by listing the objects in each set. It is conventional to use set braces when doing so.
Examples of sets:
{a, b, c, d, e, f}
{4, 9, 2, 7}
{Larry, Moe, Curly}
{cat, dog}
{1, 2, 3, 4, 5, 6, 7, ...}
{the people in this room}
NAMES FOR SETS
We will typically use upper case letters for the names of sets.
Let
A = {a, b, c, d, e, f}
B = {4, 9, 2, 7}
C = {Larry, Moe, Curly}
D = {cat, dog}
N = {1, 2, 3, 4, 5, 6, 7, ...}
F = {the people in this room}
ELEMENTS OR MEMBERS OF SETS
The contents of a set are called its elements or members.
We say "9 is an element of B"
"cat is an element of D"
Notation:
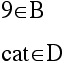
Likewise:
6 is not an element of B
dog is not an element of A

The CARDINALITY of a set is the number of elements in the set.
In general the cardinality of a set S is denoted n(S).
For example, the cardinality of set B is 4.
Notation:
n(B) = 4
Likewise n(A) = 6
n(D) = 2
n(F) is _____
n(N) is infinity?
SET EQUALITY
Two sets are said to be equal if they contain exactly the same elements.
Examples
{a, b, c} = {b, c, a}
{4, 2, 7, 9} = B
On the other hand:
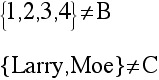
A formal definition of set equality is this:
Sets S and T are equal if every element of S is an element of T
and every element of T is an element of S.
Set-builder notation
is a formalistic way of describing the elements of a set without listing them all.
It is useful in some cases where a less formal description might be ambiguous.
EXAMPLE 1.1.1
F = {x|x is a person in this room}
We read this as follows:
"F is the set of all x such that x is a person in this room"
More examples of set-builder notation:
N = {x|x is a positive integer}
"N is the set of all x such that x is a positive integer"
New set:
E = {x|x is a positive even number}
List the elements of E.
SUBSETS
Let A = {a, b, c, d, e, f}
B = {4, 9, 2, 7}
C = {Larry, Moe, Curly}
D = {cat, dog}
E = {2, 4, 6, 8, 10, ...}
N = {1, 2, 3, 4, 5, 6, 7, ...}
F = {x|x is a person in this room}
G = {b, c, f}
Notice, for instance, that every element of G is also an element of A.
In a case like this we say "G is a subset of A"
Notation:
![]()
Likewise, ![]()
A formal definition of the word subset is this:
For sets S and T, S is a subset of T if every element of
S is also an element of T.
This means that S is contained within T.
Example
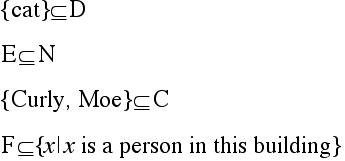
Also:
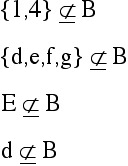
Formally: S is not a subset of T if there is at least one element of S
that is not an element of T.
EXAMPLE 1.1.2
Referring to the sets listed earlier, determine whether each statement is true or false.
1. ![]()
2. n(A) = a
3. ![]()
4. ![]()
5. ![]()
6. ![]()
7. ![]()
See solutions
Exercise #7 above illustrates a general fact about subsets:
Every set is a subset of itself.
PROPER SUBSETS
If S is a subset of T but is not equal to T, we say that S
is a proper subset of T.
Notation:
![]()
Examples:
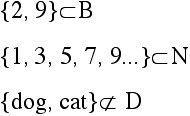
The last example illustrates this basic fact:
No set is a proper subset of itself.
COMPLEMENTS, THE UNIVERSAL SET, AND THE EMPTY SET
Consider the set S = {Moe, Larry}
Suppose we want to complete the following exercise:
List all of the elements that are NOT in S.
Are we supposed to list...
...the names of all film performers except Moe and Larry?
...the names of all stooges except Moe and Larry?
...every object on Earth except Moe and Larry?
Unless we establish some boundaries on the scope of this exercise, we cannot finish it.
To establish a frame of reference for a set problem, we
can define a universal set (U) for the problem:
For any set problem or discussion, a universal
set (U) is a "larger" set that contains all of the elements that
may be of interest in the discussion; in particular, the universal set at
least contains all of the elements of all of the sets in the discussion.
Returning to the example at hand:
Let U = {Moe, Larry, Curly, Shemp, Curly Joe}
Then to list the elements that are not in S, we
list those elements of U that are not in S:
{Curly, Shemp, Curly Joe}
This set is called the complement of S, and is
denoted ![]() .
.
THE EMPTY SET
There is a unique set that contains no elements.
It is called the empty set or the null set or the void set.
The empty set is usually denoted with one of these symbols:
{ } or ![]()
Click here for a brief discussion of nothing
EXAMPLE 1.1.3
Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
X = {2, 4, 6, 8, 10}
W = {x|x is an odd number}
Y = {3}
True or false:
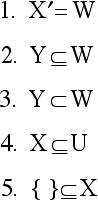
see solution
GENERAL FACT:
In any set problem, every set is a subset of U, and { } is a subset of
every set.
WWW Note:
For practice on problems involving sets, elements, subsets and the empty set, visit
The Sets Appealer
THE NUMBER OF SUBSETS IN A FINITE SET
General observation: It makes sense to assume that the more
elements a set has, the more subsets it will have.
For finite sets, there is a strict relationship between the
cardinality of a set and the number of subsets . We can discover
this relationship by filling in the following table:
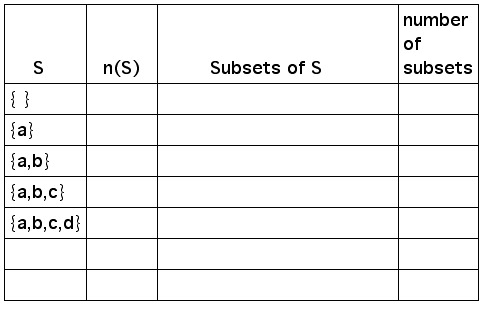
The number of subsets in a finite set
If n(S) = k, then the number of subsets in S is 2k.
EXAMPLE 1.1.4
A = {a, b, c, d, e, f}
Since n(A) = 6, A has 26 subsets.
That is, A has 64 subsets (26 = 64).
How many proper subsets does A have?
EXAMPLE 1.1.5
Let U = {1, 2, 3, 4, 5, 6, 7,...}
Let S = {x|x is less than 10}
1. How many subsets does S have?
2. How many proper subsets does S have?
see solution
WWW note:
For exercises involving the number of subsets and the number of proper subsets,
try The Subsetizer.
Download practice exercises (PDF file)