FACTORIALS, PERMUTATIONS AND COMBINATIONS
n! "n factorial"
If nis a positive integer, then n!is nmultiplied by all of the smaller positive integers.
Also, 0! = 1
![]()
0! = 1
1! = 1
2! = (2)(1) = 2
3! = (3)(2)(1) = 6
4! = (4)(3)(2)(1) = 24
5! = (5)(4)(3)(2)(1) = 120
6! = (6)(5)(4)(3)(2)(1) = 720
7! = (7)(6)(5)(4)(3)(2)(1) = 5,040
8! = (8)(7)(6)(5)(4)(3)(2)(1) = 40,320
9! = (9)(8)(7)(6)(5)(4)(3)(2)(1) = 362,880
10! = (10)(9)(8)(7)(6)(5)(4)(3)(2)(1) = 3,628,800
n! is n multiplied by all of the positive integers
smaller than n.
FACT:
n! is the number of different ways to arrange (permutations of) n objects.
EXAMPLE 1.5.1
There are four candidates for a job. The members of the search committee will
rank the four candidates from strongest to weakest. How many different outcomes are
possible?
EXAMPLE 1.5.1 SOLUTION
If you were to use the Fundamental Counting Principle, you would need to make four dependent decisions:
1. Choose strongest candidate: 4 options
2. Choose second-strongest candidate: 3 options
3. Choose third-strongest candidate: 2 options
4. Choose weakest candidate: 1 option
(4)(3)(2)(1) = 24
A shorter way to get this answer is to recognize that the problem is
asking us to find the number of ways to arrange (according to relative suitability) four people.
By definition, the number of ways to arrange 4 things is 4!
4! = 24
EXAMPLE 1.5.2
In how many ways is it possible for 15 students to arrange themselves among 15 seats
in the front row of an auditorium?
see solution
EXAMPLE 1.5.3
There are 8 greyhounds in a race. How many different orders of finish (first place through eighth place) are possible?
see solution
EXAMPLE 1.5.4
1. The password for Gomer's e-mail account consists of 5 characters chosen from the set
{g, o, m, e, r} . How many arrangements are possible, if the password has no repeated characters?
2. How many 5-character passwords are possible if a password may have repeated characters?
see solution
EXAMPLE 1.5.5
Gomer has a 20 volume set of World Book Encyclopedia. The 20 volumes are arranged in numerical order. His uncle Aristotle has challenged him to write down every possible arrangement of the 20 books. Aristotle will pay Gomer $10,000 if he can compete the job within 30 days. The only proviso is that if Gomer doesn't complete the job within 30 days, he will have to pay Aristotle 1 penny for every permutation that he has failed to list.
How many different arrangements are there?
Gomer is a fast worker. Assuming that he can write down 1 million arrangements per second, how long will it take for him to complete the job?
see solution
EXAMPLE 1.5.6
Refer to the situation in the previous example.
Use the fundamental counting principle to answer this question:
If Gomer is going to choose 9 of the 20 books, and arrange them on a shelf, how many arrangements are possible?
EXAMPLE 1.5.6 SOLUTION
We can't directly use n! to solve this problem, because in this case he is not arranging the entire set of 20 books. At this point, we must use the Fundamental Counting Principle. Gomer has to make 9 dependent decisions:
1. Choose first book: 20 options
2. Choose second book: 19 options
3. Choose third book: 18 options
4. Choose fourth book: 17 options
5. Choose fifth book: 16 options
6. Choose sixth book : 15 options
7. Choose seventh book: 14 options
8. Choose eighth book: 13 options
8. Choose ninth book: 12 options
According to the Fundamental Counting Principle, the number of different outcomes possible is
(20)(19)(18)(17)(16)(15)(14)(13)(12) = 60,949,324,800 arrangements
There is another way to get the answer to this question, without having to enter 9 numbers into the calculator. It refers to a special formula involving n!:
The PERMUTATION FORMULA
The number of permutations of n objects taken r at a time:
![]()
This formula is used when a counting problem involves both:
1. Choosing a subset of r elements from a set of n elements; and
2. Arranging the chosen elements.
Referring to EXAMPLE 1.5.6 above, Gomer is choosing and arranging a subset of 9 elements from a set of 20 elements, so we can get the answer quickly by using the permutation formula, letting n = 20 and r = 9. (That is, the answer to this problem is the number of permutations of 20 things taken 9 at a time.)
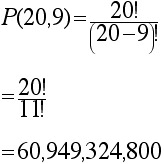
EXAMPLE 1.5.7
There are ten candidates for a job. The search committee will choose four of them, and rank the chosen four from strongest to weakest. How many different outcomes are possible?
see solution
EXAMPLE 1.5.8
There are 8 horses in a race. If all we are concerned with are the first,
second and third place finishers (the trifecta), how many different orders of
finish are possible?
see solution
EXAMPLE 1.5.9
Suppose we are going to use the symbols {a, b, c, d, e, f, g, h} to form a 5-character "password" having no repeated characters. How many different passwords are possible?
EXAMPLE 1.5.10
There are six greyhounds in a race: Spot, Fido, Bowser, Mack, Tuffy, William.
We are concerned about who finishes first, second and third. How many different 1st-2nd-3rd orders of finish are possible?
Examples:
S-B-F
M-B-S
T-W-M
M-T-W
A. 120
B. 216
C. 18
D. 15
see solution
EXAMPLE 1.5.11
Homer, Gomer, Plato, Euclid, Socrates, Aristotle, Homerina and Gomerina form the
board of directors of the Lawyer and Poodle Admirers Club. They will choose
from amongst themselves a Chairperson, Secretary, and Treasurer. No person will
hold more than one position. How many different outcomes are possible?
A. 336
B. 24
C. 512
D. 21
see solution
ASSORTED EXAMPLES:
Many of the examples from Unit 3 Module 1 could be solved with the
permutation formula as well as the fundamental counting principle.
Identify some of them and verify that you can get the correct solution by using P(n,r).
FACT:
Any problem that could be solved by using P(n,r) could also be
solved with the FCP. The advantage to using P(n,r) is that in
some cases we can avoid having to multiply lots of numbers.
Conversely, there are problems that can be solved with the
FCP but can't be solved using P(n,r).
EXAMPLE 1.5.12
Consider the set S = {a, b, c, d, e}.
1. How many different 3-letter code "words" can we form using the letters of set S without using repeated letters? Examples: abc, bca, dec, cde, bda, adb are 6 different code "words."
2. How many different 3-element subsets does S have?
Solution to #1:
We can use the FCP, since forming one of these code words requires three decisions:
i. Choose first letter (5 options)
ii. Choose second letter (4 options)
iii. Choose third letter (3 options)
According to the FCP, the number of different outcomes is (5)(4)(3) = 60 code words.
We could also use the permutation formula, since forming a three letter code word
requires us to choose and arrange three elements from a set of five elements.
Solution to #2
The answer to this problem is not 60.
Although the code words "abc," "cba," and "bac" are all
different from one another, the subsets {a, b, c}, {c, b, a} and {b, a, c} are all
the same as one another. This means that the number of 3-element
subsets must be fewer than 60.
We can list them all:
{a, b, c}
{a, b, d}
{a, b, e}
{a, c, d}
{a, c, e}
{a, d, e}
{b, c, d}
{b, c, e}
{b, d, e}
{c, d, e}
Although there are 60 different 3-element code words with no repeated letters,
there are only 10 different 3-element subsets.
There is a formula that allows us to get this result without having to
list all of the possible subsets.
We say that "10 is the number of combinations of 5
elements taken 3 at a time."
COMBINATIONS
The number of combinations of n things taken r at a time:
![]()
We use this formula when we are choosing a
subset of r elements from a set of n elements, and
the order in which elements are chosen or listed is not significant.
Example: How many 5-element subsets are in the set S = {2, 3, 4, 5, 6, 7, 8, 9}?
Answer:
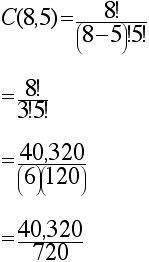
= 56 different 5-element subsets
EXAMPLE 1.5.13
Recall this problem from earlier: There are six greyhounds in a
race: Spot, Fido, Bowser, Mack, Tuffy, William. How many different 1st-2nd-3rd place
orders of finish are possible? We saw that the answer was P(6,3) = 120.
New question: After the race, three dogs will be randomly chosen for veterinary examination.
How many different three-dog groups are possible?
see solution
EXAMPLE 1.5.14
A pizzeria is offering a special: for $6 you get a four-topping pizza.
The choices for toppings are pepperoni, sausage, olives, mushrooms, anchovies, peppers, and onions.
How many different 4-topping combinations are possible
(assuming that no topping can be repeated on a pizza)?
see solution
EXAMPLE 1.5.15 Classic example of combinations
The Florida Lotto Saturday night drawing used to work like this:
There are 49 ping-pong balls in a machine, each bearing a number from 1 to 49.
The machine randomly spits out 6 ping-pong balls. If the numbers on the ping-pong balls match
the six numbers that you chose, YOU WIN!
How many different outcomes are possible?
Now, the Lotto works like this: there are 53 balls instead of 49.
How many outcomes are possible under this new scheme?
see solutions
EXAMPLE 1.5.16
Poor choice of words: the device that we commonly call a combination lock would more accurately be called a permutation lock or a fundamental
counting principle lock.
Why? Because, for one of these locks, the correct "combination" is
determined not only by the numbers that are selected, but also by the order in
which they are selected.
Suppose "combination" lock has a dial whose numbers are 1 through 16.
Assuming that repeated numbers are allowed within a "combination", how
many different 3-number "combinations" are possible?
(For example, 10-13-10, 8-12-2, 2-12-8 are three different possibilities.)
How many possibilities would there be if repeated numbers were not allowed?
GENERAL WARNING: Our everyday use of the word "combination" does not always agree with the mathematical meaning of that word.
EXAMPLE 1.5.17
There are nine people on the Board of Directors of the Gomermatic Investment Corporation (GIC). At the onset of their monthly board meeting, each person shakes hands with each of the other people. How many handshakes occur?
see solution
EXAMPLE 1.5.18
Harpo, Groucho, Chico, Zeppo, Gummo, Karl, and Skid have won three tickets to the opera. They will randomly choose three people from their group to attend the opera. How many outcomes are possible?
Suppose that instead of choosing 3 people to attend the opera, they decide instead to choose 4 people to not attend. How many outcomes are possible?
see solution
EXAMPLE 1.5.19
Gomer has eight pet wolverines. He has won a gift certificate to Wally's Wolverine World, that entitles him to one free wolverine massage, one free wolverine shampoo, and one free wolverine manicure. Gomer will randomly select which wolverines receive the treats described above.
1. How many different outcomes are possible, if we assume that no wolverine will receive more than one treat?
A. 512
B. 256
C. 56
D. 336
2. How many different outcomes are possible, if we assume that it may be possible for a wolverine to receive more than one treat?
A. 512
B. 256
C. 56
D. 336
see solution
EXAMPLE 1.5.20
Euclid's Auto Body Shoppe is trying to unload some unwanted paint by offering the following special deal: for $99 you get a two-tone paint job, using one color for the top and a different color for the body. The available colors are: hot pink, puke green, Gator orange, flaming chartreuse. How many different paint schemes are possible?
A. 8
B. 16
C. 12
D. 7
see solution
EXAMPLE 1.5.21
A jar contains a penny, a nickel, a dime, a quarter, a half-dollar, and a silver dollar. Three coins are selected (without replacement) and their monetary sum is determined. How many different monetary sums are possible? (Examples: dime, quarter, penny: 36¢; nickel, half-dollar, dollar: $1.55.)
A. 36
B. 120
C. 60
D. 20
see solution
EXAMPLE 1.5.22
Is it A. P(8,3); B. C(8,3); C. 83; or D. 38 ?
There are 8 kittens in a pet shop:
1. Three kittens will be randomly selected and donated to a nursing home. How many different three-kitten collections are possible?
2. One kitten will be chosen for a rabies vaccination, one kitten will be chosen for a distemper shot, and one kitten will be declawed. In how many different ways can the choice of kittens be made, if it is possible that more than one of these treatments may be given to the same kitten?
3. One kitten will be chosen for a rabies vaccination, another kitten will be chosen for a distemper shot, and a third kitten will be declawed. In how many different ways can the choice of kittens be made?
4. Each kitten will be given either a red, blue, or green ribbon. How many outcomes are possible?
see solution
EXAMPLE 1.5.23
Is it P(9,5), C(9,5) or 95?
Each item below can be answered with either A. P(9,5); B. C(9,5); or C. 95
Choose the correct answer in each case.
1. The number of 5-element subsets in a 9-element set = ____
2. The number of 5-symbol codes that can be formed using the symbols
{@, /, $,¿, &, ß, £, à, ? } if repeated symbols are allowed = _____.
3. The number of different ways to choose 5 people from a set of 9 and position them in 5 seats = _____.
4. The number of ways to choose a chairperson, associate chairperson, parliamentarian, treasurer, and secretary from a list of 9 candidates = _____ (assuming that no person will hold more than one office).
5. The number of different 5-person groups that can be chosen from a collection of 9 people = _____.
6. The number of 4-element subsets in a 9-element set = _____.
see solution
The heavy-metal band Death Maggot normally performs 10 songs during a concert. One night, however, they found that they would only have enough time to perform 7 songs, due to the fact that their opening act got called back for three encores. If the band randomly chooses 7 songs to play, how many different outcomes are possible?
On the other hand, if they randomly choose 3 songs not to play, how many different outcomes are possible?
Assuming that they are only going to play 7 songs from their 10-song repertoire, how many different arrangements are possible?
see solution
Download practice exercises (PDF file)