LOGIC: Statements, Negations, Quantifiers, Truth Tables
Statements
A statement is a declarative sentence having truth value.
Examples:
Today is Saturday.
Today I have math class.
1 + 1 = 2
3 < 1
Some cats have fleas.
All lawyers are dishonest.
Today I have math class and today is Saturday.
1 + 1 = 2 or 3 < 1
For each of the sentences listed above (except the one that is stricken out) you should be able to determine its truth value (that is, you should be able to decide whether the statement is TRUE or FALSE).
Symbols for statements
It is conventional to use lower case letters such as p, q, r, s to represent logic statements. Referring to the statements listed above, let
p: Today is Saturday.
q: Today I have math class.
r: 1 + 1 = 2
s: 3 < 1
u: Some cats have fleas.
v: All lawyers are dishonest.
Note: In this course, when we encounter a subjective or value-laden term (an opinion) such as "dishonest," we will assume for the sake of the discussion that that term has been precisely defined.
Click here for a philosophical discussion of statements and opinions
Quantified statements
The words "all" "some" and "none" are called quantifiers.
A statement containing one or more of these words is a quantified statement.
Note: the word "some" means "at least one."
EXAMPLE 2.1.1
According to your everyday experience, decide whether each statement is true or false:
1. All dogs are poodles.
2. Some books have hard covers.
3. No U.S. presidents were residents of Georgia.
4. Some cats are mammals.
5. Some cats aren't mammals.
see solutions
EXAMPLE 2.1.1*
True story: in the spring of 1999, a man in Tampa, Florida was diagnosed with stomach cancer. He underwent surgery to have the cancer removed. During this procedure, the surgical team discovered that in fact there was no cancer after all; the original diagnosis was incorrect. After the surgery, the physicians told the patient "All of the cancer has been removed." Did the physicians lie?
See solution
NEGATIONS
If p is a statement, the negation of p is another statement that is exactly the opposite of p.
The negation of a statement p is denoted ~p ("not p").
A statement p and its negation ~p will always have opposite truth values; it is impossible to conceive of a situation in which a statement and its negation will have the same truth value.
Example:
Let p be the statement "Today is Saturday."
Then ~p is the statement "Today is not Saturday."
On any given day, if p is true then ~p will be false; if p is false, then ~p will be true.
It is impossible to conceive of a situation in which p and ~p are simultaneously true;
it is impossible to conceive of a situation in which p and ~p are simultaneously false.
Negations of quantified statements
Fact: "None" is the opposite of "at least one."
Example: The negation of "Some dogs are poodles" is "No dogs are poodles."
Notice that "Some dogs are poodles" is a statement that is true according to our everyday experience, and "No dogs are poodles" is a statement that is false according to our everyday experience.
In general:
The negation of "Some A are B" is "No A are B."
(Note: this can also be phrased "All A are the opposite of B," although this construction sometimes sounds ambiguous.)
EXAMPLE 2.1.2
Write the negation of "Some used cars are reliable."
See solution
EXAMPLE 2.1.4
TRUTH TABLES
TAUTOLOGIES
More negations of quantified statements
Fact: "Some aren't" is the
opposite of "all are."
Example: The negation of "All goats are mammals" is "Some goats aren't mammals."
Notice that "All goats are mammals" is a statement that is true according to our everyday experience,
while "Some goats aren't mammals" is a statement that is false
according to our everyday experience.
In fact, it is logically impossible to imagine a
situation in which those two statements have
the same truth value.
In general, the negation of "All A are B" is "Some A aren't B."
EXAMPLE 2.1.3
Write the negation of "All lawyers are clever."
See solution
Write the negation of "No crabs are cuddly."
See solution
WWW NOTE:
For practice in recognizing the negations of quantified statements,
try
The Quantifier-er.
LOGICAL CONNECTIVES
The words "and" "or" "but" "if...then" are
examples of logical connectives. They are words that can be used to connect
two simple statements to form a more complicated compound statement.
Examples of compound statements:
"I am taking a math class but I'm not a math major."
"If I pass MGF1106 and I pass MGF1107 then my liberal studies
math requirement will be fulfilled."
EQUIVALENT STATEMENTS
Any two statements p and q are logically equivalent if
they have exactly the same meaning.
This means that p and q will always have the
same truth value, in any conceivable situation.
If p and q are equivalent statements,
then it is logically impossible to imagine a situation in which
the two statements would have differing truth values.
Examples:
"Today I have math class and today is Saturday"
is equivalent to
"Today is Saturday and today I have math class."
This equivalency follows simply from our everyday understanding of the meaning ot the word "and."
"This and that" means the same as "That and this."
Likewise,
"I have a dog or I have a cat"
is equivalent to
"I have a cat or I have a dog"
This equivalency follows simply from our everyday understanding of the meaning ot the word "or."
"This or that" means the same as "That or this."
Logical equivalence is denoted by this
symbol: 
Referring back to examples 1.4.1 #4 and #5 we saw that the statment
"Some cats are mammals" was true, while the statement "Some cats aren't mammals" was false.
This means that those two statements are NOT equivalent.
The pair of statements cited above illustrate this general fact:
"Some A are B"
is not equivalent to
"Some A aren't B."
THE CONJUNCTION AND THE DISJUNCTION
The conjunction:
If p, q are statements, their conjunction is the statement "p and q."
It is denoted: 
Example
Let p: "I have a dime."
Let q: "I have a nickel:
Then is "I have a dime and I have a nickel."
In general, in order for 
to be true, both p and q must be true.
Example: "Tallahassee is in Florida and Orlando
is in Georgia" is a false statement.
More on the conjunction
The word but is also a a conjunction;
it is sometimes used to precede a negative phrase.
Example:
I've fallen and I can't get up"
means the same as
"I've fallen but I can't get up."
In either case, if p is "I've fallen" and q is "I can get up" the conjunction above is symbolized as
The disjunction:
If p, q are statements, their disjunction is the statement "p or q."
It is denoted: 
Who's to blame?
Example:
Let p be "Today is Tuesday"
Let q be "1 + 1 = 2"
Then 
is the statement "Today is Tuesday or 1 + 1 = 2."
In order for a disjunction to be true,
at least one of its two parts must be true.
The only time a disjunction is false is when both parts are false.
The statement "Today is Tuesday or 1 + 1 = 2" is TRUE.
Equivalencies for the conjunction ("and")
and the disjunction ("or")
According to our everyday usage of the words "and" and "or" we have the following equivalencies:
1. "p and q" is equivalent to "q and p"
2. "p or q" is equivalent to "q or p"
Examples:
"I have a dime or I have a nickel"
is the same as
"I have a nickel or I have a dime."
"It is raining and it isn't snowing"
is the same as
"It isn't snowing and it is raining."
EXAMPLE 2.1.6
Suppose p and q are true statements, while r is a false statement.
Determine the truth value of
1. 
2. 
3. 
Solution for EXAMPLE 2.1.6 #2
We are given the statement 
where q is true, r is false. Substitute the value T for the variable q, and the value F for the variable r:
Now, evaluate the expression inside the parentheses.
A conjunction is only true in the case where both of its simpler parts are true,
so in this case the expression inside the parentheses is false.
Now the statement simplifies to: ~(F)
The negation of false means the opposite of false, which is true.
So, the truth value of the given statement, under the given conditions,
is TRUE.
See solutions to #1 and #3
WWW Note:
For unlimited practice problems involving the truth values of symbolic statements,
go to Mr. Wooland's home page and try The Logicizer
Note: you may want to wait until after you've read Unit 1 Module 5 before trying this.
A truth table is a device that allows us to
analyze and compare compound logic statements.
Consider the symbolic statement: 
Whether this statement is true or false depends upon
whether its variable parts are true or false.
Later, we will make a truth table for this statement.
A truth table for this statement will take
into account every possible combination of the variables
being true or false, and show the truth value of the compound
statement in each case.
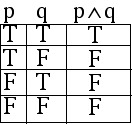
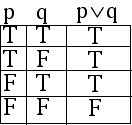
EXAMPLE 2.1.7
As an introduction, we will make truth tables for
these two statements
1.
2.
Solution to EXAMPLE 2.1.7 #1
Solution to EXAMPLE 2.1.7 #2
1. The number of rows in the truth table depends upon
the number of basic variables in the compound statement.
To determine the number of rows required, count the number of
basic variables in the statement, but don't re-count
multiple occurrences of a variable.
1 variable---2 rows
2 variables--4 rows
3 variables--8 rows
4 variables--16 rows and so forth.
2. The number of columns in a truth table depends upon the
number of logical connectives in the statement.
A. There will be one column for each basic variable; and
B. To determine the number of other columns, count the number of
logical connectives in the statement;
do re-count multiple occurrences of the same connective.
In addition to the columns for each basic variable,
there will usually be one column for each
occurrence of a logical connective.
3. The beginning columns are filled in so
as to take into account every possible combination of the
basic variables being true or false.
Each row represents one of the possible combinations.
4. In order to fill in any other column in the truth table, you must refer to a previous column or columns.
EXAMPLE 2.1.7 #3
Make a truth table for the following statement:
see solution
EXAMPLE 2.1.8
Make truth tables for the following statements:
1. 
2. 
See solution to EXAMPLE 2.1.8 #1
See solution to EXAMPLE 2.1.8 #2
WWW Note:
For unlimited practice problems involving truth tables,
go to Mr. Wooland's home page and try The Truth Tabler
Note: you may want to wait until after you've read Unit 1 Module 5 before trying this.
Referring to the truth table for the statement 
to be false.
A tautology is a statement that cannot possibly be false, due to its logical structure (its syntax).
The statement 
is a example of a tautology.
EXAMPLE 2.1.9
Is the statement 
a tautology?
We can answer this question by making a truth table.
See solution
EXAMPLE 2.1.9A
Is the statement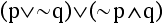 
a tautology?
We can answer this question by making a truth table.
See solution
EXAMPLE 2.1.10
Compare the truth table column for 
(EXAMPLE 2.1.8 #1) to the column for 
(this is the second column from the right in the solution for EXAMPLE 2.1.8 #2).
Solution to EXAMPLE 2.1.10
In making the comparison, we see that the two columns are identical: each column has "T" in the first row, "T" in the second row, "F" in the third row, and "T" in the fourth row. When two statements have identical truth table columns, the statements are equivalent.
USING TRUTH TABLES TO TEST FOR LOGICAL EQUIVALENCY
To determine if two statements are equivalent, make a truth table having a
column for each statement. If the columns are identical, then the statements are equivalent.
From EXAMPLE 2.1.10, we see that
EXAMPLE 2.1.12
Use the result from EXAMPLE 2.1.10 to write a statement that is equivalent to "It is not
the case that both I won't order a taco and I will order a burrito."
Solution to EXAMPLE 2.1.12
If p represents "I will order a taco" and q
represents "I will order a burrito" then the statement "It is not the case that both
I won't order a taco and I will order a burrito" is symbolized as 
.
The result from EXAMPLE 2.1.10 tells us that 
is equivalent to 
: "I will order a taco or I won't order a burrito."
EXAMPLE 2.1.14
1. Use a truth table to determine whether 
is equivalent to 
.
2. Use a truth table to determine whether 
is equivalent to 
.
3. Use a truth table to determine whether 
is equivalent to 
.
4. Use a truth table to determine whether 
is equivalent to 
.
See solution
EXAMPLE 2.1.15
Complete the following truth table.
Identify any equivalencies or tautologies.
See solution
EXAMPLE 2.1.16
Make a truth table for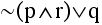 
See solution
DeMORGAN'S LAWS
From example 1.4.12 #2 and 1.4.12 #4 we have the following rules of logical equivalency:
These two rules are called DeMorgan's Laws for Logic.
Although they are written as equivalencies, in fact they tell us how to write the negation of an conjunction or disjunction.
The negation of a conjunction:
The negation of "p and q" is "not p or not q."
The negation of a disjunction:
The negation of "p or q" is "not p and not q."
EXAMPLE 2.1.17
Use DeMorgan's Laws to write the negation of each statement:
1. I want a car and a motorcycle.
2. My cat stays outside or it makes a mess.
3. I've fallen and I can't get up.
4. You study or you don't get a good grade.
Solution to Example 1.4.17
1. I don't want a car or I don't want a motorcycle.
2. My cat doesn't stay outside and it doesn't make a mess.
3. I haven't fallen or I can get up.
4. You don't study and you get a good grade.
EXAMPLE 2.1.18
1. Select the statement that is the negation of "Today is Monday and it isn't raining."
A. Today isn't Monday and it isn't raining.
B. Today isn't Monday or it isn't raining.
C. Today isn't Monday or it is raining.
D. Today isn't Monday and it is raining.
E. Today is Friday and it is snowing.
2. Select the statement that is the negation of "I'm careful or I make mistakes."
A. I'm not careful and I don't make mistakes.
B. I'm not careful or I don't make mistakes.
C. I'm not careful and I make mistakes.
D. I'm not careful or I make mistakes.
E. I never make misteaks.
See solution
EXAMPLE 2.1.19
1. Select the statement that is the negation of "I walk or I chew gum."
A. I don't walk and I chew gum.
B. I don't walk or I chew gum.
C. I don't walk and I don't chew gum.
D. I don't walk or I don't chew gum.
E. I walk until I step on chewed gum.
2. Select the statement that is the negation of "I'm mad as heck and I'm not going to take it anymore."
A. I'm not mad as heck and I'm not going to take it anymore.
B. I'm not mad as heck or I'm not going to take it anymore.
C. I'm not mad as heck and I am going to take it anymore.
D. I'm not mad as heck or I am going to take it anymore.
3. Select the statement that is the negation of "All of the businesses are closed."
A. Some of the businesses are closed.
B. Some of the businesses are not closed.
C. None of the businesses are closed.
D. All of the businesses are open.
E. All of my clothes are businesslike.
4. Select the statement that is the negation of the statement "Some pilots are pirates."
A. All pilots are pirates.
B. No pilots are pirates.
C. Some pilots are not pirates.
D. All pirates are pilots.
See solution
EXAMPLE 2.1.20
'But wait a bit,' the Oysters cried,
'Before we have our chat;
For some of us are out of breath,
And all of us are fat!'
"No hurry!' said the Carpenter.
They thanked him much for that.
Select the statement that is the negation of "Some of us are out of breath,
and all of us are fat."
A. Some of us aren't out of breath or none of us is fat.
B. Some of us aren't out of breath and none of us is fat.
C. None of us is out of breath and some of us aren't fat.
D. None of us is out of breath or some of us aren't fat.
see solution
ANOTHER EQUIVALENCY FOR THE "OR" STATEMENT
Consider this disjunction: "You will behave or you won't get a reward."
Can you think of another statement that conveys exactly the same meaning without using the word "or"?
Fact: any statement of the form "p or q" can be written equivalently in the form "If not p, then q." This is denoted 
and will be discussed in detail in Module 1.5
A summary of facts about the conjunction and the disjunction.
Equivalencies
Statement Equivalent form p and q q and p
p or q q or p
p or q If not p then q
Negations (DeMorgan's Laws)
Statement Negation p and q not p or not q
p or q not p and not q
EXAMPLE 2.1.21
Select the statement that is logically equivalent to "I'm careful or I make mistakes."
A. I'm careful and I make mistakes.
B. I make mistakes and I'm careful.
C. If I'm not careful, then I make mistakes.
D. None of these.
see solution
DIAGRAMMING CATEGORICAL STATEMENTS
Diagramming is a technique involving the use of Venn diagrams to study the relationships between multiple categorical statements.
It is particularly useful in situations involving two or three categories, and two or more categorical statements.
When diagramming a universal statement, such as "All dogs are mammals" or Ò"No dogs are cats," we use
shading to indicate that a certain region of the diagram must contain no elements.
When diagramming an existential statement, such as "Some dogs are poodles" or Ò"ome dogs aren't scavengers," we use an "X" to indicate that a certain region of the diagram must contain at least one element. If it is not certain which of two regions must contain an element, then we place an ÒXÓ on the border between the two regions.
If a region of a marked diagram contains no marks, then it is uncertain whether that region contains any elements.
EXAMPLE 2.1.22
Mark the diagram according to the statement "No dogs are cats."
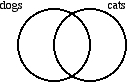
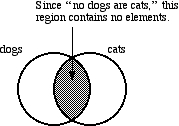
SOLUTION
If "no dogs are cats," then the part of the diagram where those two circles intersect must contain no elements. We use shading to indicate that a region of the diagram must contain no elements.
EXAMPLE 2.1.23
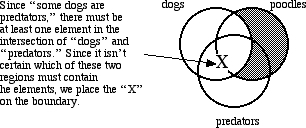
Mark the diagram according to both of these statements: "All poodles are dogs" and "Some dogs are predators."
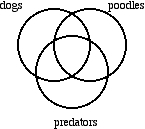
SOLUTION
First, the universal statement "All poodles are dogs" asserts, indirectly, that a certain region of the diagram must contain no elements (and this is the only thing that such a statement asserts; in particular, a universal statement never asserts the existence of any elements).
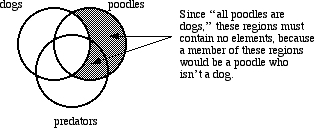
Next, continue marking the diagram according to the existential statement "Some dogs are predators." This means that there must be at least one element in the part of the diagram that is where "dogs" and "predators" intersect.
EXAMPLE 2.1.24
Suppose the marked diagram below conveys information about relationships between pirates, ruffians and scoundrels. We use shading to indicate that a region contains no elements. An "X" in a region indicates the existence of at least one element; an "X" on the boundary between two regions indicates that the union of those two regions contains at least one element. If a region is unmarked, then whether that region contains any elements is uncertain. Select the choice that must be true according to the marked diagram.
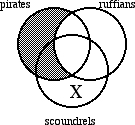
A. No pirates are ruffians and some ruffians aren't scoundrels.
B. No pirates are ruffians and some scoundrels aren't ruffians.
C. All pirates are ruffians and some ruffians aren't scoundrels.
D. All pirates are ruffians and some scoundrels aren't ruffians.
E. None of these is correct.
See solution
Download practice exercises (PDF file)