PART 2 MODULE 4
CATEGORICAL SYLLOGISMS
AND DIAGRAMMING
Consider the following
argument:
Some lawyers are judges.
Some judges are politicians. Therefore, some lawyers are
politicians.
Although the premises and
conclusion of this argument sound reasonable, and although the structure of the
argument looks similar to transitive reasoning, this argument is invalid.
In order to show that the
argument is invalid, all we have to do is conceive of a situation in which the
conclusion is false, while both premises are true. In order to do so, it
helps if we imagine a world with a small population of lawyers, judges and
politicians. Suppose there are only two lawyers, Alice and Bill, and that
Bill is also a judge, but Alice isn't. Suppose that in addition to Bill
there is only one other judge, Carla, and Carla is also a politician, but Bill
isn't a politician. Finally, suppose there is one other politician, Don,
who isn't a lawyer and isn't a politician. In this conceivable world, some
lawyers are judges (Bill), and some judges are politicians (Carla), but no
lawyers are politicians. Since it is possible to conceive of a situation
in which the conclusion is false while both premises are true, this argument is
invalid.
The previous argument is an
example of a CATEGORICAL SYLLOGISM,
which is an argument involving two premises, both of which are categorical
statements. Categorical
statements are statements of the form "all are...," "none
are..." or "some are..." A categorical statement of the
form "all are..." is also called a positive universal statement. A categorical statement of the form
"none are..." is also called a negative universal statement. A categorical statement of the
form "some are..." or “some aren’t is also called an existential
statement.
In this discussion we are
primarily concerned with categorical syllogisms in which at least one premise
is an existential statement, because such arguments cannot be analyzed using
the methods of Unit 2 Module 1.
Existential statements
A statement of the form
"Some are...," such as "Some lawyers are judges," is
conceptually quite different from a universal statement, in that it cannot be
restated in terms of logical connectives in any way that is of practical use. Whereas
a positive universal statement such as "All cats are mammals" can be
informally restated as "If __ is a cat, then __ is a mammal," and
whereas a negative universal statement such as "No cats are dogs" can
be restated as "If __ is a cat, then __ isn't a dog," it is not
possible to make such a transition with an existential statement such as “Some
mammals are predators.”
This means that the
techniques of Unit 2 Module 1, which are based on truth tables and logical
connectives, are of no use for arguments involving the existential statement.
Diagramming categorical
statements
There is an extensive
literature on the topic of categorical syllogisms, dating back to medieval
scholarship and earlier. This includes an impressive body of special
terminology, symbols, and characterizations of forms, which a student might
encounter in a more intense study of the subject, such as in a history of
philosophy course.
This discussion will be
limited to the presentation of a method of analyzing categorical syllogisms
through the use of three-circle Venn diagrams. This method is
called diagramming.
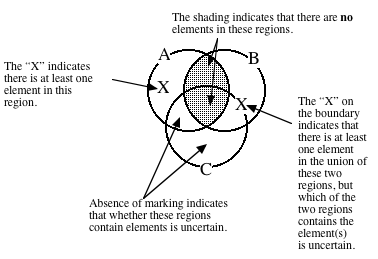
Individual statements are
diagrammed as follows.
1. Use shading to
diagram universal statements, by shading out any region that is known to
contain no elements.
2. Use an
"X" to diagram an existential statement. If a region is known
to contain at least one element, place an "X" in that region.
If it is uncertain which of two regions must contain the element(s), then
place the "X" on the boundary between those two regions.
3. If a region
contains no marking, then it is uncertain whether or not that region contains
any elements.
The marked Venn diagram
below illustrates these ideas.
Diagramming categorical
syllogisms
To test the validity of a
categorical syllogism, follow these steps.
1. In order to be
valid, a categorical syllogism must have at least one premise that is a
universal statement. If none of the premises is a universal statement,
then the argument is invalid, and we are done. The following steps assume
that at least one premise is a universal statement.
2. Begin by
diagramming the universal premise(s). A universal statement will have the
effect of shading (blotting out, so to speak) some region of the diagram,
because a universal statement will always assert, directly or otherwise, that
some region of the diagram has no elements.
3. Confining your attention
to the part of the diagram that is unshaded,
diagram an existential premise by placing an "X" in a region of the
diagram that is known to contain at least one element. If it is uncertain
which if two regions should contain the element(s), place the "X" on
the boundary between those two regions.
4. After diagramming the
premises, if the diagram shows the conclusion of the argument to be true, then the
argument is valid. If the diagram shows the conclusion to be uncertain or
false, then the argument is invalid.
5. If all the
statements in the argument are universal statements, then the argument can be
analyzed in terms of transitive reasoning or false chains (see Unit 2 Module
1), and so diagramming is unnecessary.
6. If the both remises are universal statements but the conclusion is an
existential statement, then the argument is invalid. No diagram is necessary. You cannot deduce “some” from “all” or “none.”
EXAMPLE A
Use diagramming to test the
validity of this argument:
No terriers are timid.
Some bulldogs are terriers. Therefore, some bulldogs are not timid.
SOLUTION
We will mark this
three-circle Venn diagram, which shows the sets "terriers,"
"bulldogs" and "timid (things):"
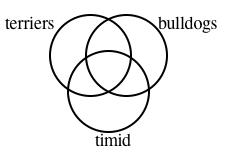
First, diagram the negative
universal premise "No terriers are timid." According to this
premise, the overlap of those two sets contains no elements, so that part of
the diagram is shaded, or "blotted out."
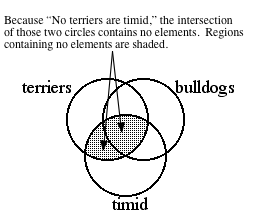
Next, diagram the
existential premise "Some bulldogs are terriers" by placing an
"X" in the appropriate location in the unshaded portion of the
diagram.
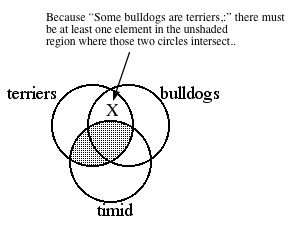
Now that both premises have
been diagrammed, check to see if the marked diagram shows the conclusion to be
true.
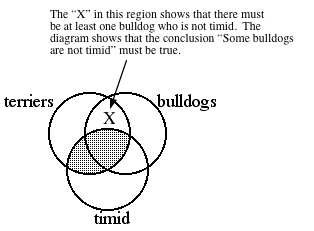
Because the marked diagram
shows that the conclusion is true, the argument is valid.
EXAMPLE B
Use diagramming to test the
validity of this argument.
Some useful things are
interesting. All widgets are interesting. Therefore, some widgets
are useful.
SOLUTION
We can use this
three-circle Venn diagram, shows the sets of widgets, interesting (things) and
useful (things):
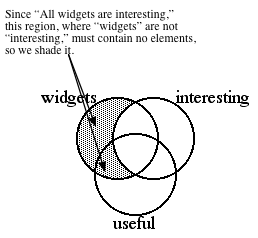
Start by diagramming the
universal premise, "All widgets are interesting."
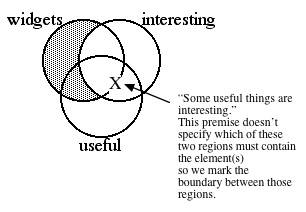
Next, diagram the
existential premise, "Some useful things are interesting." This
means that there must be at least one element in the overlap of those two
circles. However, that overlap entails two regions, and it is uncertain
as which of those two regions contains the element(s), so we place an
"X" on their border.
Now that we have diagrammed
both premises, we check to see if the marked diagram shows the conclusion,
"Some widgets are useful," to be true.
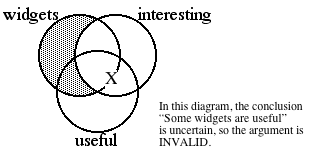
The argument is invalid, because the diagram shows that, based on those
premises, the conclusion is not certain.
That is, the “X” is not in the part of the diagram where “widgets” and
“useful” intersect.
EXAMPLE 2.3.1
Test the validity of this argument:
All elephants are huge creatures.
Some huge creatures have tusks.
Therefore, some elephants have tusks.
EXAMPLE 2.3.1 SOLUTION
Use shading to diagram the universal premise “All elephants are huge creatures.” Shading indicates that a region has no elements.
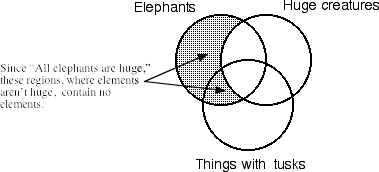
Next, use an “X” to diagram the existential premise “Some
huge creatures have tusks.”
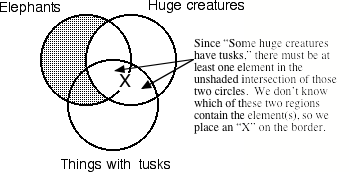
Now that both premises have been diagrammed, if the marked diagram shows that the conclusion is true, then the argument is valid. If the marked diagram shows that the conclusion is false or uncertain, then the argument is invalid.

EXAMPLE 2.3.2
Test the validity of the argument:
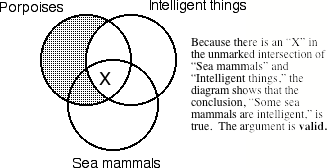
All porpoises are intelligent. Some sea mammals are porpoises. Therefore, some sea mammals are intelligent.
EXAMPLE 2.3.2 SOLUTION
First use shading to diagram the universal premise.
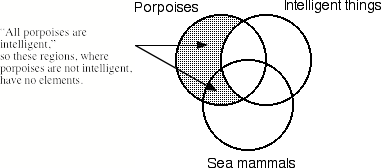
Next use an “X” to diagram the existential premise.
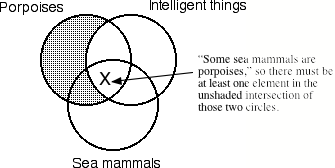
If the marked diagram shows that the conclusion is true,
then the argument is valid. If the
marked diagram shows that the conclusion is uncertain or false, then the
argument is invalid.
EXAMPLE 2.3.3
Test the validity of the argument:
All cows like to chew. Some dairy animals don't like to chew.
Therefore, some dairy animals aren't cows.
EXAMPLE 2.3.4
Test the validity of the argument:
Some lawyers are judges. Some judges are politicians. Therefore, some lawyers are politicians.
WORLD WIDE WEB NOTE
For practice on arguments involving categorical syllogisms and diagramming, visit the companion website and try The CATEGORIZER.
EXAMPLE 2.3.6
Test the validity of each argument.
A. Some fish are tasty. All fish can swim. Therefore, some tasty things can swim.
B. Some doctors are dentists. Some dentists are surgeons. Therefore, some doctors are surgeons.
C. All hogs are smelly. Some swine aren't hogs. Therefore, some swine aren't smelly.
D. All burglars are criminals. Some thieves are criminals. Therefore, some burglars are thieves.
E. Some food preparers aren't cooks. All chefs are cooks. Some food preparers aren't chefs.
F. No thieves are saintly. Some congressmen are thieves. Therefore, some congressmen aren’t saintly.
EXAMPLE 2.3.7
Consider these premises:
All poodles are dogs. All dogs bark.
We should easily recognize that a valid conclusion is "All poodles bark."
Question: since "All poodles bark" is a valid conclusion, wouldn't "Some poodles bark" also be a valid conclusion? After all, "some" sounds like a softer condition than "all," so common sense suggests that "some A are B" should be a valid conclusion whenever "all A are B" is a valid conclusion.
However, the answer to the question above is "no." In fact, "all" does not imply "some," due to this peculiarity of the word "all:" A statement like "All poodles bite" is true even if there were no poodles. In other words, if all of the poodles went extinct, the statement "All poodles bite" would still be (vacuously) true, but the statement "Some poodles bite" would be false (because "some poodles bites" means that there must be at least one poodle).
This example gives rise to the following observation, which holds for all arguments.
If every premise in an argument has the form "All are...," or “None are…” a valid conclusion will not have the form "Some are..." (unless a premise specifies that all of the sets in the argument are non-empty).