EXAMPLE 3.5.1**

According to a recent article from the New England Journal of Medical Stuff ,

63% of cowboys suffer from saddle sores,

52% of cowboys suffer from bowed legs,

40% suffer from both saddle sores and bowed legs.

What is the probability that a randomly selected cowboy has saddle sores and bowed

legs?

Let's answer this question correctly, using the Multiplication Rule.

SOLUTION

Let E be the event that a cowboy has saddle sores. Let F be the event that a cowboy has bowed legs. We are trying to find P(E and F), for two dependent events (a cowboy with saddle sores is more likely to also have bowed legs).

In this expression, we know that P(E) = .63 (63% of the cowboys have saddle sores).

We need to know P(F, given E); that is, we need to know the probability that a cowboy has bowed legs, given that he has saddle sores. The following Venn diagram can help:

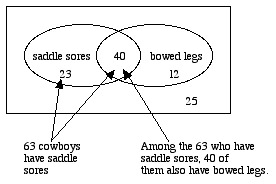
This shows that the probability that a cowboy has bowed legs, given that he has saddle sores [P(F, given E)] is 40/63.

Now we can use the Multiplication Rule correctly:

The Multiplication Rule will always yield the correct result, as long as we take into account whether the events are dependent or independent.