
MONICA K.
HURDAL
|


MONICA K.
HURDAL
|
I am working on creating flat maps of the human brain. The surface of the brain is a very complicated surface with many folds (gyri) and fissures (sulci). The individual variablilty in the shape and size of the gyri and sulci of each person's brain makes it difficult to compare brains across subjects to determine significant regions of function and activation. As a result, it is important to look at new ways to visualize anatomical and functional information.
The surface of the brain, or grey matter, is where the functional activation
of the brain occurs and one way of visualizing the activity of the brain
is to create a surface-based map. To do this, one begins by obtaining a
representation of the surface of the cortex. For example, a region of the
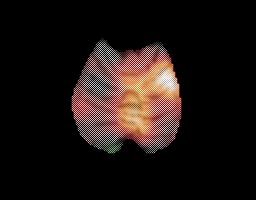
brain is isolated in a magnetic resonance imaging (MRI) volume by stripping
away all the undesired regions. For example, the cerebellum can be isolated
by stripping away the scalp, skull, cerebrospinal fluid and cerebrum in
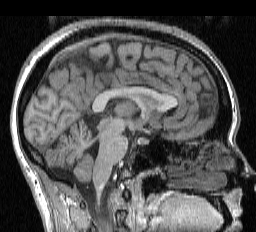
an MRI volume. The cerebellum is located in the
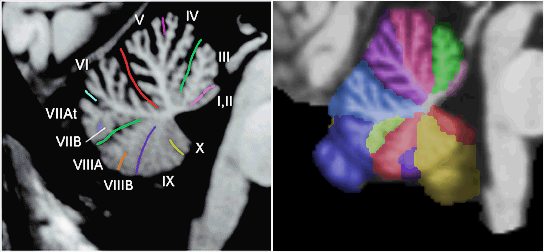
lower left part of the following image. The next image illustrates various
regions which have been color coded for identification purposes.
The surface from the region of interest is obtained by creating a
triangulated representation of the isolated surface, using a variant of the
marching cubes algorithm. One of the difficulties is that the resulting surface
must be topologically correct and have no defects. This means that the
surface must be equivalent to a sphere: it can have no holes or no bridges
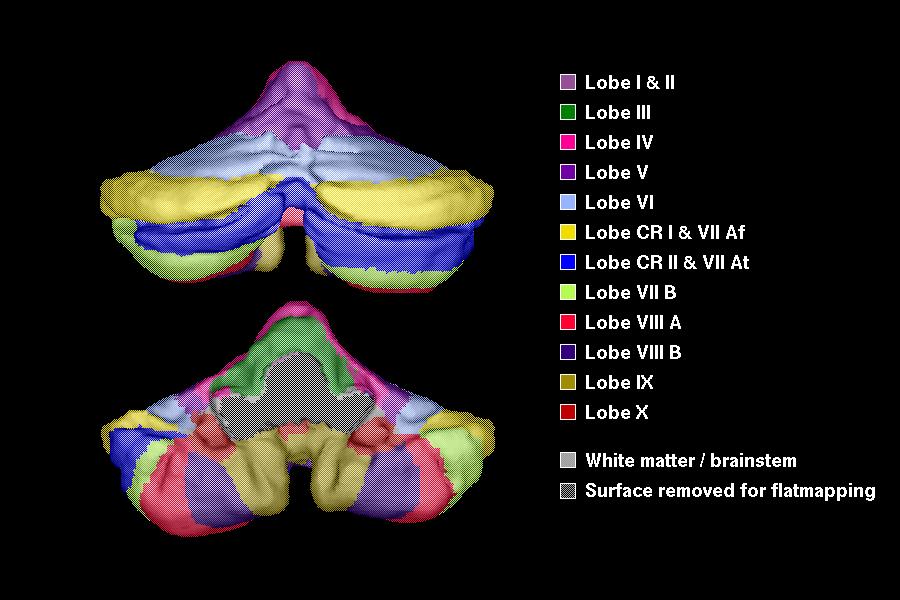
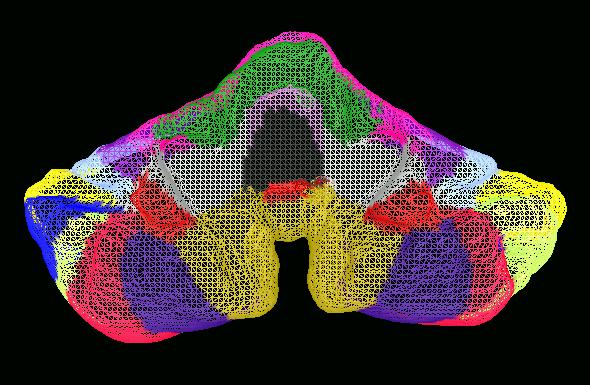
(handles). Here is an example of the surface representing the
human cerebellum that was obtained. Various lobes and fissures have been
color-coded in the same manner as on the MRI slice.
Since the surface is so intricate and complicated, one method of simplifying the way of looking at the surface is to create a flat map of the brain. This is analagous to creating a flat map of the surface of the earth. It is impossible to flatten a surface in 3D without introducing areal and linear distortion. Nevertheless, a common way to flatten the surface of the brain is to attempt to reduce the areal and / or linear distortion between the original surface and the flattened surface.
However, it is possible to flatten a surface such that the angular distortion is zero when given two points or a point and a direction (the Riemann Mapping Theorem). This is known as a conformal map (when angle proportion and angle direction between the original surface and the flattened surface is preserved). We take the unique approach of implementing the Riemann Mapping Theorem to create a map of the brain which attempts to preserve the conformal structure between the original surface and the flattend surface. To do this, we use the concept of circle packing.
A circle packing is a configuration
of circles with a specified pattern of tangencies. Circle packings
can be used for approximating conformal mappings of a piecewise flat surface to
a flat map in the plane.
Let K represent a simply-connected triangulated surface which is a
2-manifold (ie. no hold and no handles). Then there exists a circle packing
for K on the Riemann sphere. This circle packing is unique up to
Möbius transformations and inversions of the Riemann sphere.
Furthermore, this packing represents a discrete conformal map (1).
A packing for K is created as follows. Each vertex, v,
of K is represented by a circle cv with the center
of cv located at v. If vertices v
and w are connected by an edge, then the circles cv
and cw are tangent.
Vertex v belongs
to k triangle faces, giving k angles at v. The sum of
these angles is defined to be the angle sum of v,
 (v).
A set of circles can be "flattened" so they fit together in the plane if
(v).
A set of circles can be "flattened" so they fit together in the plane if
 (v) = 2Pi.
This is accomplished by iteratively refining the circle packing and adjusting
each angle at v. This process is repeated for all interior vertices
until a nominated accuracy in the angle sums is achieved. More details of
this method can be found in my poster.
The maps which are produced using this approach are quasi-conformal as there
is a bounded amount of angular distortion. We are currently working on ways
of reducing the amount of angular distortion to create more conformal maps.
(v) = 2Pi.
This is accomplished by iteratively refining the circle packing and adjusting
each angle at v. This process is repeated for all interior vertices
until a nominated accuracy in the angle sums is achieved. More details of
this method can be found in my poster.
The maps which are produced using this approach are quasi-conformal as there
is a bounded amount of angular distortion. We are currently working on ways
of reducing the amount of angular distortion to create more conformal maps.
Here are some example of flat maps of the cerebellum which I have created.
Functional PET information was obtained from a target interception task. Here
are some axial, coronal and sagittal images from this task.

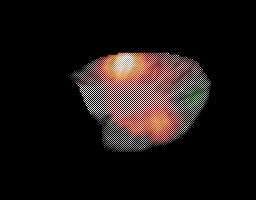
This information can be imposed on the flat maps. One of the benefits of
circle packing, is that you can create maps in different geometries, such as
in the Euclidean plane, in the hyperbolic plane or on a sphere. Here is a map
in the Euclidean plane. It shows the various anatomical regions of the
cerebellum and has the functional regions from the target interception task
imposed onto it.

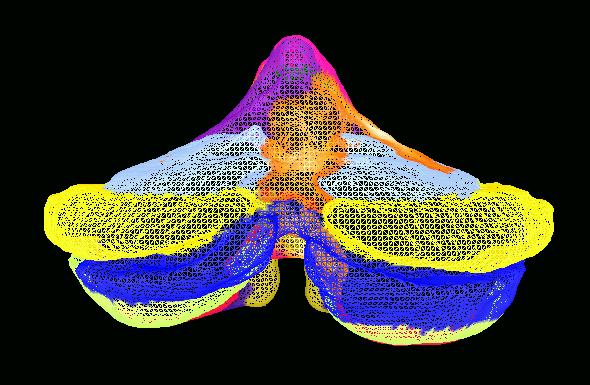
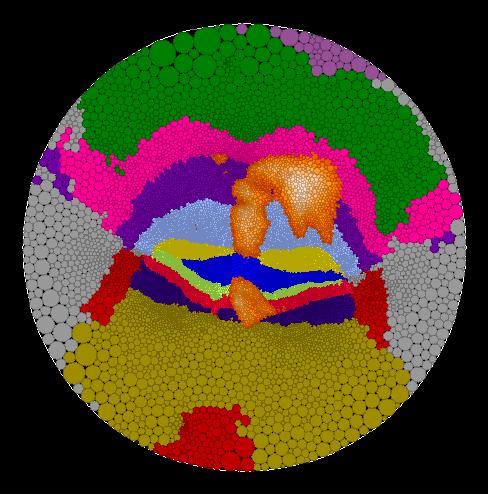
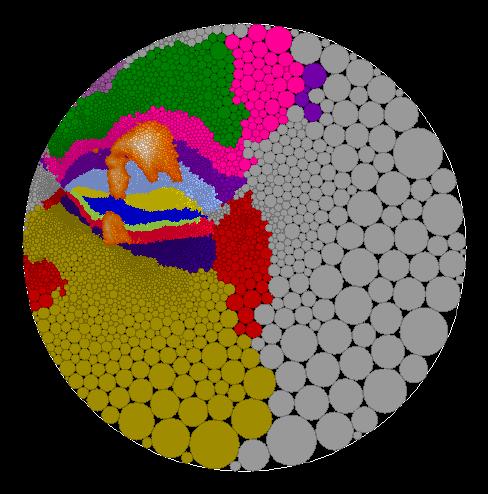
One of the advantages of creating maps in the hyperbolic plane is that
you can interactively change the map focus to alter to regions of high map
distortion. Because we look at a hyperbolic map with Euclidean eyes, to us
the center (or focus) of the hyperbolic map appears to have little distortion
while the distortion increases as you move out to the edge of the map. For
example, the center of the hyperbolic map on the left is marked in black.
If the second black black circle located in the lower portion of the left map
is used as a new map focus, then the map on the right is obtained. The
new focus is indicated in the center of the map on the right and the old
focus of the left map is indicated in black in the upper portion of the right
map.
See some pictures of hyperbolic maps of the Earth to understand how the distortion changes on these types of maps.
Maps can also be created on a sphere. Here are two different views:
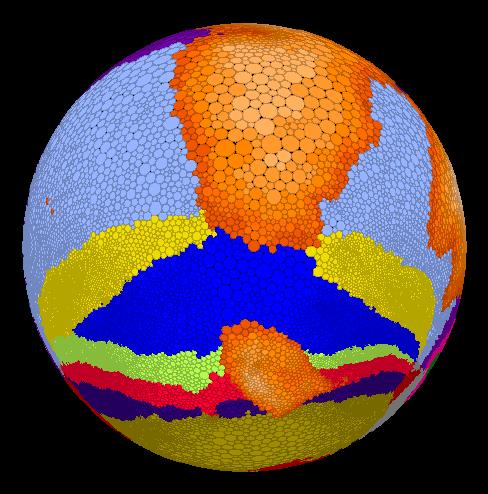

For other pictures of maps on the sphere, click here.
For some older pictures of flat maps of the cerebellum that were created using an older cutting method (which has now been abondoned), click here.
This approach of creating flat maps of the brain offers several advantages over existing approaches including:
Eventually we expect to make this software for creating flat maps of the brain freely available to researchers. If you are interested in being updated regarding the status and availablitly of this software, please email me at mhurdal@math.fsu.edu and I'll add you to my list. Similarly, if you would like to collaborate with us in this research, by offering data which you would like to have flat mapped, please contact me - I would be most interested in hearing from you!