Lecture 5: Properly Convex Geometry

In this lecture, we will discuss the geometry of properly convex subsets of \(\mathbb{R} P^n\). We begin by discussing an important invariant from 1-dimensional projective geoemtry that will be the basis for a metric on properly convex domains.

###The Cross Ratio

Recall that we can identify \(\mathbb R P^1\) with \(\mathbb R \cup \{\infty\}\). Suppose that \(a,x,y,b\in \mathbb R P^1\) are a 4 distinct points, then we can define the cross ratio as

where a limit is taken if one of the points is \(\infty\). The cross ratio has many useful properties which we now outline.

1. If the points occur in order (with respect to the orientation on \(\mathbb R P^1\)) then \([a:x:y:b]>1\).
2. If \(A\in PGL_2(\mathbb R)\) then \([Aa:Ax:Ay:Ab]=[a:x:y:b]\)
3. If \([a:x:y:b]=[a':x':y':b']\) then there is a unique \(A\in PGL_2(\mathbb R)\) such that \(A\cdot(a,x,y,b)=(a',x',y',b')\)
4. If \((a,x,z,y,b)\) is an ordered quintuple of points in \(\mathbb R P^1\) then \([a:x:y:b]=[a:x:z:b][a:z:y:b]\)

All of the above properties can be verified by elementary computations. Property 2 shows that the cross ratio is a projective invariant of quadruples of points and property 3 can be thought of as saying that this invariant uniquely determines quadruples of points in \(\mathbb R P^1\).

Property 4 can be viewed as a metric property. Specifically, the cross ratio allows us to put a metric on the interval \((a,b)\) using the formula \(d_{ab}(x,y)=\log([a:x:y:b])\) for \(x,y\in (a,b)\). Property 4 ensures that this metric satisfies the triangle inequality. We now discuss some comparison properties of this metric

Let \(a,x,y,b\in \mathbb{R}P^1\) be ordered, then we can think of \([a:x:x+t:b]\) and \([a:x:y:a+t]\) as functions of \(t\). I simple computation involving derivatives shows that

1. \([a:x:x+t:b]\) is increasing for \(t\in (0,b-x)\)
2. \([a:x:y:a+t]\) is decreasing for \(t\in (y-1,\infty)\)

The first property shows that as points move away from each other on \((a,b)\) that the their distance increases, and the second property shows that the metric gets smaller as the interval gets larger.

The following cross ratio identity in \(\mathbb{R}P^2\) will also be of much use to us. For \(1\leq i\leq 4\), let \(\ell_i\) be four lines passing through a common point, \(p\in \mathbb{R}P^2\) and \(a_i\) and \(b_i\) be quadruples of concurrent points, as in the image below.

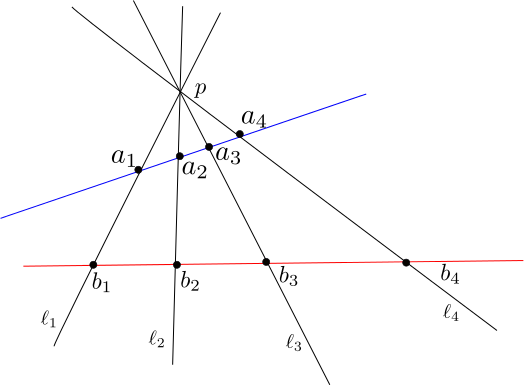
Then \([a_1:a_2:a_3:a_4]=[b_1:b_2:b_3:b_4]\). This can be seen as follows: there is a projective transformation fixing \(p\) and mapping \(a_i\) to \(b_i\) for \(1\leq i\leq 3\). Such a transformation leaves the lines \(\ell_1,\ell_2\), and \(\ell_3\) invariant. However, it is easy to see that such a projective transformation must leave \(\ell_4\) invariant as well (the \(\ell_i\) correspond to 4 concurrent points in \(\mathbb{R}P^{1\ast}\)), and as such it must map \(a_4\) to \(b_4\). It should be remarked that the quantity we are calculating is really just the cross ratio of the concurrent lines \(l_1,l_2,l_3,l_4\) when regarded as element of \(\mathbb{R}P^{2\ast}\).

###The Hilbert Metric

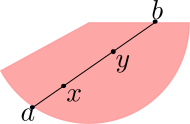
Let \(\Omega\subset \mathbb{R}P^n\) be an open properly convex domain and let \(x,y\in \Omega\). Since \(\Omega\) is properly convex the projective line connecting \(x\) and \(y\) intersects \(\partial \Omega\) in two points \(a\) and \(b\) and we define the Hilbert distance betwee these points as

It is easy to see that \(d_\Omega(x,y)=0\) if and only if \(x=y\) and that \(d_\Omega(x,y)=d_\Omega(y,x)\). Furthermore, since projective maps preserve the cross ratio, we see that elements of \(PGL(\Omega)\) are isometries. We now discuss why \(d_\Omega\) satisfies the triangle inequality. The triangle inequality follows from a comparison argument with a triangle \(\Delta\subset \mathbb{R}P^2\), and so for the time being we assume that \(d_\Delta\) satisfies the triangle inequality.

Let \(x,y,z\in \Omega\). Any three such points are contained in a projective 2-plane that intersects \(\Omega\), thus the proof can be reduced to the two dimensional case. The key point is that we can always find a triangle \(\Delta\) such that \(d_\Omega(x,z)=d_\Delta(x,z)\), \(d_\Omega(z,y)=d_\Delta(z,y)\), and \(d_\Omega(x,y)\leq d_\Delta(x,y)\). This is illustrated in the following picture.

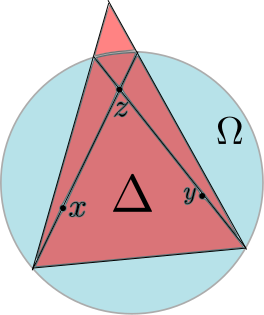
As a result we see that

We now verify that the triangle inequality is satisfied for triangular domains in \(\mathbb{R}P^2\). This will be done by showing that for a triangle \(\Delta\), \((\Delta,d_\Delta)\) is isometric to \((\mathbb{R}^2,d_{Hex})\), where \(d_{Hex}\) is the metric on \(\mathbb{R}^2\) coming from the norm whose unit ball is a regular hexagon.

We can realize a projective triangle as

If we realize \(\mathbb{R}^2\) as the plane in \(\mathbb{R}^3\) where the coordinates sum to zero, then there is a map \(L:\Delta\to \mathbb{R}^2\) given by \([e^{c_1},e^{c_2},e^{c_3}]\mapsto (c_1,c_2,c_3)\). The group of diagonal matrices in \(SL_3(\mathbb{R})\) with positive entries acts as a transitive group of isometries on \(\Delta\) with respect to the Hilbert metric. For any such diagonal matrix \(A\), a simple computation shows that \(L\circ A\) is a translation of \(\mathbb{R}^3\) that preserves \(\mathbb{R}^2\), and is thus a \(d_{Hex}\) isometry. It thus suffices to show that metric balls in \(\Delta\) centered at \(p_0=[1,1,1]\) are mapped by \(L\) to metric balls in \(\mathbb{R}^2\) centered at \((0,0,0)\) of the same radius.

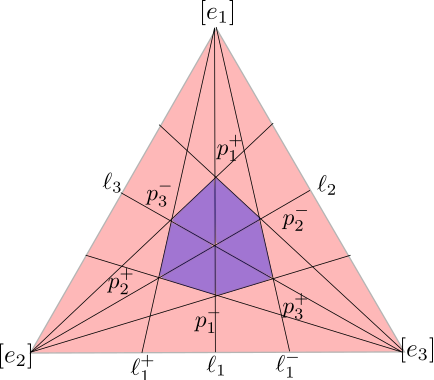
Let \(d>0\), for \(1\leq i\leq 3\) let \(\ell_i\) be the line connecting \([e_i]\) to the midpoint of the opposite side of \(\Delta\), and let \(p_i^{\pm}\) be the points on \(\ell_i\) distance \(d\) from \(p_0\) (where \(p_i^+\) is the point closer to \([e_i]\)). Let \(\ell_i^\pm\) be the line starting at \([e_i]\) and passing through \(p_{i\pm 1}^+\), where the indices are taken mod 3.

The line \(\ell_1\) can be parameterized as \([e^{2t/3},e^{-t/3},e^{-t/3}]\), and a simple computation shows that this is an isometric embedding of \(\mathbb{R}\) to \(\ell_1\). Consequently, the points \(p_{1}^\pm=[e^{\pm 2d/3},e^{\mp d/3},e^{\mp d/3}]\)

By construction, the points \(p_i^\pm\) are on the boundary of the unit ball centered at \(p_0\). These points span a hexagon \(H\) (shown in blue above) in \(\Delta\) and using the above identity for cross ratios we see that the points on the boudnary of \(H\) are distance d from \(p_0\) and thus \(H\) is the unit ball centered at \(p_0\). Furthermore, the six sides of this \(H\) are contained in the lines \(\ell_i^\pm\).

Consider the line

This line has \([e_2]\) as one of its endpoints and its a simple computation shows that its intersection with \(\ell_1\) is \(p_1^-\), and so we see that \(\ell=\ell_2^+\). A similar argument shows that

As a result, we see that The images of \(\ell_i^{\pm}\) under \(L\) are lines in \(\mathbb{R}^2\) that span a hexagon in \(\mathbb{R}^2\). Furthermore, the \(L\)-image of the \(d\)-ball centered at \(p_0\) is obtained by scaling the \(L\)-image of the 1-ball centered at \(p_0\) by a factor of \(d\). As a result we see that \(L\) is an isometry. Consequently, \(d_\Delta\) satisfies the triangle inequality, and thus \((\Delta, d_\Delta)\) is a metric space.

An interesting and fun fact that can be easily verified from the above picture is that for this metric \(\pi\) (i.e. the ratio of the circumfrence and the diameter of a circle) is 3.

Previous Post: Lecture 4: Projective Structures and Maps

Next Post: Lecture 6: Benzécri's compactness theorem