UNIT 3 MODULE 6

INDEPENDENT EVENTS, THE MULTIPLICATION RULES, CONDITIONAL PROBABILITY



EXAMPLE 3.6.1

Suppose we have one six-sided die, and a spinner such as is used in a child's game. When we spin the spinner, there are four equally likely outcomes: "A," "B," "C," and "D."

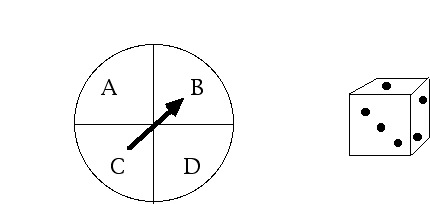
An experiment consists of rolling the die and then spinning the spinner. The face of the spinner has four congruent regions, labeled "A," "B," "C," and "D," respectively.
How many different outcomes are possible?

What is the probability that the outcome will be "3-C?"

We will discuss the "impossibility of Tuesday" after we've introduced some preliminary facts.



Suppose we roll one die.

Let A be the event that the result is the number "2."

Then we know that

P(A) = 1 divided by 6
However, suppose that before I reveal the result of the die roll, I tell you that an even number has occurred (event E).

Would you still say that

P(A) = 1 divided by 6?
This is an example of CONDITIONAL probability.

We say that

"The probability that the die roll is '2,' given that the die roll is 'even,' is 1 divided by 3, because if we know that an even number has been rolledm then there are only three possible outcomes, one of which is a "2."

or, P(A, given B) = 1 divided by 3.

General fact:

For any events E, F
P(B, given A) = (number of outcomes favorable to both A and B) divided by (number of outcomes favorable to A).

which is the same as

P(B, given A) = P(A and B) divided by P(A).



If we are referring to population statistics,

P(B, given A) = (portion of population satisfying both A and B) divided by (portion of population satisfying A)

EXAMPLE 3.6.10

In a box we have a bunch of puppies:

4 brown bulldogs

2 gray bulldogs

5 brown poodles

3 gray poodles

If one puppy is selected, what is the probability that the puppy is...

1. ...brown?

2. ...a poodle?

3. ...gray or a bulldog?

4. ...brown and a bulldog?

5. ...a bulldog, given that it is gray?

6. ...brown, given that it is a poodle?







see solutions

















EXAMPLE 3.6.11

A survey of Gators indicates that 7% are charming, 4% are modest, and 3% are both charming and modest. Find the probability that a Gator is modest, given that he/she is charming.

A. .75
B. .03
C. .43
D. .25



Solution. We apply the formula P(B, given A) = P(A and B) divided by P(A).
In this case, we have
P(modest, given charming) = P(modest and charming) divided by P(charming)
= .03 divided by .07
= .43





























EXAMPLE 3.6.12

Refer to the data on scholarships in the table presented earlier (see EXAMPLE 3.6.9).

Note: here is a summary of the data needed to answer the follwing question.
62% of students received no scholarship.
32% of students received a partial scholarship.
6% of students received a full scholarship.
1. What is the probability that a randomly-chosen student received a full scholarship, given that he/she received some sort of scholarship?

Answer.
Let A be the event "A randomly selected student received a full scholarship."
Let B be the event "A randomly selected student received a scholarship."
P(B, given A) = (portion of population satisfying both A and B) divided by (portion of population satisfying A)
= 6% divided by 38%
= .158.






EXAMPLE 3.6.14

Recently, Gomer took his Yugo to Honest Al's Yugo Repair Shop for a brake job.

Later, while driving home, a wheel fell off of the car. When Gomer returned to Honest Al's to complain that the wheel must have fallen off because of the brake job was done incorrectly, Honest Al produced a ream of statistics from NHTSA that showed that for this type of brake job, the probabilty that the wheel will fall off, even if the work is done incorrectly, is only about 0.008.

Based on that data, Honest Al graciously offered to cover 1% of the cost of repairing the damage to Gomer's car.

What question should Gomer have asked?

Answer.
Gomer should have asked a question that takes into account that the wheel has fallen off. That is, in this case the event "Wheel falls off" is not some random event that may or may not occur. It is an event that has definitely occurred. A meaningful question would be such as, "Given that the wheel has fallen off, what's the probability the work was done incorrectly?

A closer look at the data reveals the following breakdown.
There were a total of 1516 cases.
In 1 case, the wheel fell off (event F) and the work was done correctly (event C).
In 5 cases, the wheel fell off (event F) and the work was done incorrectly (event "not C").
In 860 cases, the wheel didn't fall off (event "not F") and the work was done correctly (event C).
In 655 cases, the wheel didn't fall off (event "not F") and the work was done incorrectly (event "not C").

Gomer wants to know the probability that the work was done incorrectly, given the the wheel fell off.
That is, P(not C, given F). Since there were 6 cases in which the wheel fell off, and in 5 of these case the work was done incorrectly, we have
P(not C, given F) = 5 divided by 6 = .83.
In other words, the likelihood that Honest Al is at fall is closer to 83% than it is to 1%.













EXAMPLE 3.6.15

Suppose that the data below comes from the FBI Uniform Crime Statistics.

It conveys information about the number of Americans (per 100,000 population) involved in the crimes of toad theft and toad smoking.


Per 100,000 population: 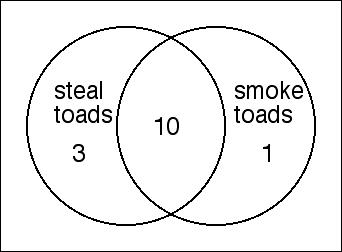Note: the Venn diagram shows the follwing breakdown.
Out of every 100,000 people, there are
10 who steal toads and smoke toads.
3 who steal toads but don't smoke toads.
1 who smokes toads but doesn't steal toads.
A rare, exotic toad has been stolen from the Tallahassee Museum. Police are searching for Gomer, who is the only known toad-smoker in town. Meanwhile, Gomer's lawyers have spoken out publicly. Referring to the data shown above, they state that, since only 10 out 100,000 people are both toad-stealers and toad-smokers, it is extremely unlikely that Gomer is the guilty party, and so the police should focus their investigation elsewhere.

What do you think about this claim?

Answer. The "10 out of 100,000" statistic would be useful if we were refering to some individual randomly selected from the general population. But that statistic is meaningless in this case, because we are referring to a specific person about whom we have special knowledge. Any meaningful statement about probability regarding that individual must take into account what is known: in this case, it is known that Gomer is a toad smoker. The relevant statement in probability would be this:
"Given that a person smokes toads, the probability that he also smokes toads is 10 out of 11." If one is going to cite statistics in support of or against Gomer, it would be more reasonable to say that the probability that he stole the toad is 10 out of 11."



































EXAMPLE 3.6.16

This situation actually occurred in Southern California a few years ago: a woman (we'll refer to her as "Nicole") was brutually murdered. The prime suspect was her ex-husband, a celebrity who had a record of domestic violence during their short-lived marriage. The ex-husband's defenders issued the following statistically reasonable statement: "Even if a woman has been the victim of domestic abuse at the hands of her husband, the probability that she will be murdered by her husband is only 1 in 1000. Therefore, it is extremely unlikely that [Mr. ex-Husband] committed the murder."

What, if anything, is wrong with this use of statistics?



see answer



















EXAMPLE 3.6.18

An IRS auditor has a list of 12 taxpayers whose tax returns are questionable. The inspector will choose 2 of these people to be audited. Eight of the taxpayers are Floridians and 4 are Georgians. What is the probability that both people selected will be Floridians?





Let E be the event that the first selectte is a Floridian. Then P(E) = 8 over twelve, because there are 12 people, 8 of whom are Floridians.
Let F be the event that the second selectee is a Floridian. Assuming that the first selectee was Floridian, then the probability that the second selectee will be Floridian is 7 over 11, because now there are 11 people to choose from, 7 of who are Floridian. Now we have
P(E and F) = (8 over 12) divided by (7 over 11) = 56 over 132.

Notice that in applying the multiplication rule in this case, the second number, 7 over 11, was actually a conditional probability. It was the P(second person is Floridian, given that first person was Floridian) , or simply P(F, given E).
This illustrates how we use the Multiplication Rule in the more general setting where that events aren't necessarily independent.









THE MULTIPLICATION RULE FOR DEPENDENT EVENTS.

If E and F are dependent, then

P(E and F) = P(E) times P(F, given E).

This rule is especially useful when we have a two-step experiment where the outcome of the first step affects the possible outcomes for the second step, such as the previous example.













INDEPENDENT vs. DEPENDENT EVENTS

In a case where two or more items are selected from a large population of unspecified size, we will assume that the selections are INDEPENDENT. In a case where two or more items are selected from a small population of specified size, we will assume that the selections are DEPENDENT.











EXAMPLE 3.6.19

In his pocket, Gomer has 3 red, 5 orange and 2 blue M&Ms.

If he randomly chooses two M&Ms, what is the probability that both will be red?

A. .6
B. .09
C. .067
D. .52



Solution.
Let E be the event that the first candy is red. The P(E) = 3 over 10, because there are 10 candies, 3 of which are red.
Let F be the event that the second candy is red. Assuming that the first candy was red, then 9 candies remain, 2 of which are red, so
P(F, given E) = 2 over 9.
So we have
P(E and F) = P(E) times P(F, given E) = (3 over 10) times (2 over 9)
= 6 over 90
or 1 over 15 in lowest terms. The best choice is C.









































EXAMPLE 3.6.20

The Skuzuzi Kamikaze sport/utility vehicle is manufactured at two plants, one in Japan and one in the US. Sixty percent of the vehicles are made in the US, while the others are made in Japan. Of those made in the US, 5% will be recalled due to a manufacturing defect. Of those made in Japan, 3% will be recalled.

Find the probability that a vehicle will be...

1. ...made in the US and not recalled.

2. ...made in Japan and recalled.





see solution

































EXAMPLE 3.6.21

The state insurance commission revealed the following information about the Preferential Insurance Company's homeowners' insurance: 10% of the policy-holders have filed more than 5 claims over the past two years; 60% of these people have had their insurance canceled; 90% of the policy-holders have filed 5 or fewer claims over the past two years; 15% of these people have had their insurance canceled.



What is the probability that a policy holder filed more than 5 claims over the past 2 years and had his/her insurance canceled?

Once again, let's turn our attention to this scenario from Unit 3 Module 5:

EXAMPLE 3.5.1**

According to a recent article from the New England Journal of Medical Stuff ,
63% of cowboys suffer from saddle sores,
52% of cowboys suffer from bowed legs,
40% suffer from both saddle sores and bowed legs.

What is the probability that a randomly selected cowboy has saddle sores and bowed legs?

We know that the answer is .40, because that information is stated directly in the problem. Earlier we saw, however, that if we try to derive this answer by using the Multiplication Rule for Independent Events, we fail because (.63)(.52) is NOT equal to .40.


Let's try again, using the correct version of the Multiplication Rule.




see solution









Download practice exercises (PDF file)